هذه بداية مقال أطول.
المحتوى: “
لا يُعدّ علماء الرياضيات عادةً أول من يلجأ إليه عند يوم النقل. ولماذا يجب أن يكونوا كذلك؟ فلمدة ستين عاماً تقريباً، لم يتمكنوا حتى من إخبارك ما إذا كان أريكتك الجديدة ذات المقاعد الثلاثة ستمر من الزاوية الضيقة إلى شقتك.
لكن جينيون باك قد يغير رأينا في ذلك. فقد قام هذا المتحمس لعلم التوافقيات والهندسة من جامعة يونسي في كوريا بنشر برهانٍ مكوّن من 100 صفحة حول هذه المشكلة تحديداً، مُحلاً بذلك إحدى أكثر المشاكل إلحاحاً في الكون، حتى نتمكن جميعاً من اتخاذ خيارات أثاث أفضل قبل أن نعلق في أعلى درج الطابق الثالث.
في عام 1966، صاغ عالم الرياضيات النمساوي الكندي ليو موزر مشكلةً تُعاني منها البشرية منذ أن وقف أسترالوبيثكس منهكاً في أقصى أرجاء كهفٍ يحمل جيفة غزال تبدو مريحة لكنها لا تتحرك أكثر.
”
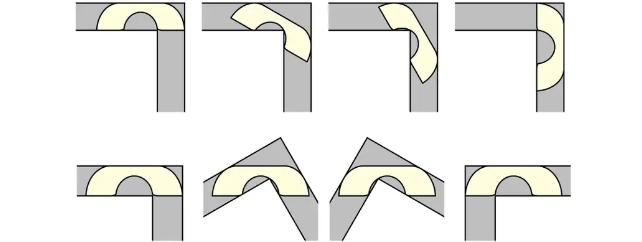
يبدو الأمر بسيطًا للوهلة الأولى. ما هو أكبر جسم ثنائي الأبعاد يمكنه أن يتجاوز زاوية على شكل حرف L بنجاح؟
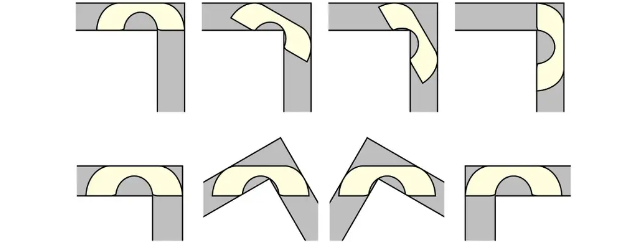

لكوريدور عرضه وحدة واحدة، فإن كرسيًا مساحته وحدة مربعة أمر سهل. من ناحية أخرى، من الواضح أن مستطيلاً مساحته وحدتان مربعتان سيتعثر. دعونا ننسى أي شيء أطول – فهو الآن يعيش في الممر.
ولكن ماذا لو كان شيئًا فريدًا من ايكيا اسمه مثل شخصية من سيد الخواتم وشكله يشبه سماعة هاتف قديمة؟
بعد عامين فقط من قيام موزر بإلقاء القفاز، وجد عالم الرياضيات البريطاني جون هامرسلي أريكة تتكون من نصف دائرة مجزأة مفصولة بمربع مُزال منه جزء على شكل نصف دائرة (حيث يمكن لثلاثة أصدقاء أن يلمسوا ركبهم بشكل محرج أثناء حديثهم في الرياضيات) يمكن أن تبلغ مساحتها 2.2074 وحدة، وما زالت قادرة على المرور من الزاوية.
كما وضع هامرسلي حدًا أعلى للتصميم – لا شيء أكبر من 2.8284 يمكنه المرور.
مر ما يقرب من ربع قرن قبل أن يقترح باحث من جامعة روتجرز يدعى جوزيف جيرفر إعادة تصميم دقيقة لأريكة هامرسلي، بتقريب بعض الحواف بأقواس إضافية، ليجد شكلاً أضاف أجزاءً كسرية إلى الحد الأدنى السابق، مدعياً أن أقصى حجم للأريكة هو جزء بسيط يزيد عن 2.2195 وحدة.
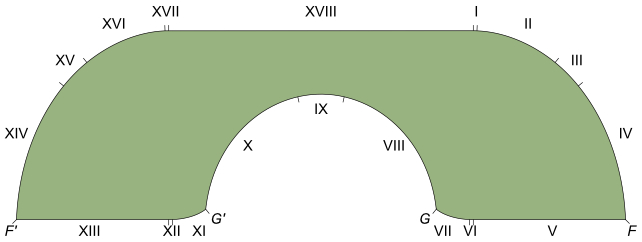
لكن، وبدون وجود صيغة عالمية لأشكال الأرائك تصف جميع الأبعاد الممكنة للأثاث، يصعب إثبات أن أريكة أكبر قليلاً ذات انحناءات مختلفة قليلاً قد لا تناسب.
في عام 2018، استخدم عالم الرياضيات يواف كالوس من معهد سانتا فيه، ودان روميك من جامعة كاليفورنيا، ديفيس، مخططًا بمساعدة الكمبيوتر لإظهار أن ارتفاع الأريكة يمكن أن يصل إلى 2.37 وحدة.
ولإثبات هذه النتيجة الأخيرة، استخدم باك بعضًا من السحر الرياضي المعروف باسم الدالة الحقنية لإنشاء خريطة لأشكال أريكة جيرفر الناجحة، محددًا الخصائص الرئيسية قبل توسيعها عبر أبعاد أكبر لإثبات مرة واحدة وإلى الأبد مدى ضخامة أريكة تشبه أريكة جيرفر.
وبالتأكيد، فإن 2.2195 وحدة هي ملك الأرائك لممر عرضه وحدة واحدة وزاوية على شكل حرف L، كما اقترح جيرفر في عام 1992.
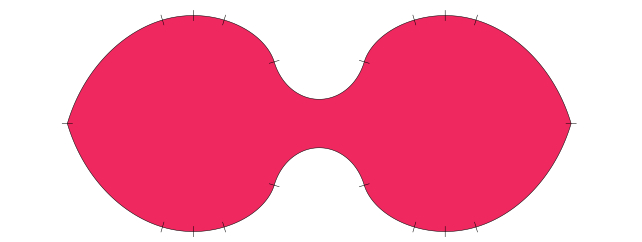
على الرغم من أنه لم تتم مراجعته بعد من قبل الأقران، إلا أن حل باك قد يكون الكلمة الأخيرة في مشكلة الأريكة، على الأقل في هذا الإطار. إذا كان لديك زاوية ثانية لتدور في الاتجاه المعاكس، فنحن نوصي بشَكل يُسمى أريكة روميك ثنائية الاستخدام.
متوفرة الآن في الممر 13 في ايكيا، بجانب طاولة مطبخ غيملي.
هذا القسم الأخير من مقال أطول. بحث متوفر على خادم ما قبل النشر arXiv.
المصدر: المصدر