”

تتعدد أهداف العلم، إلا أنها جميعًا تندرج تحت المفهوم الواسع لفهم ووصف واقعنا بدقة متناهية. فإذا أعطيتنا وضعًا ما، وأخبرتنا بالشروط الأولية لذلك النظام الفيزيائي، فبقدر ما تكون أفضل النظريات العلمية لدينا قوية، سيتمكن العلم من التنبؤ بدقة لكيفية تطور ذلك النظام في المستقبل. وإذا استطعنا قياس ومعرفة خصائص أي شيء نتعامل معه، من الذرات إلى البشر إلى الكواكب إلى النجوم والمجرات وأكثر، فستتمكن نظرية علمية مفيدة من التنبؤ بكيفيتها بعد فترة زمنية محددة من الآن.

لكن في بعض الأحيان، يتطلب فهم ماهية النظرية العلمية، وما تفعله، أو حتى معناها، أن نتعلم بعض المصطلحات التي لسنا على دراية بها، بما في ذلك المصطلحات التي لها جذورها في الرياضيات وغالبًا ما لا تكون بديهية. قد تسمع كلمات مثل الكميات القياسية، والمتجهات، والموترات تُطرح، ولكن نادرًا ما ترى شرحًا واضحًا ومقنعًا لما هي هذه الأشياء في الواقع. هذه المجالات ذات أهمية حيوية في كل من الفيزياء الكلاسيكية والفيزياء الكمية، سواء للجسيمات الفردية، وأيضًا، وربما بشكل أكثر جوهرية، للمجالات التي تخترق كل الفضاء. هنا، بأبسط وأوضح المصطلحات التي يمكننا جمعها، ماهية المجال القياسي (أبسط أنواع المجالات) في الواقع، وما الذي يخبرنا به.

يُظهر كوكب الأرض، كما رصده مسبار مسنجر التابع لناسا عند مغادرته موقعنا، بوضوح طبيعته الكروية. وهذه ملاحظة لا يمكن إجراؤها من نقطة مراقبة واحدة على سطحه.

لنقل إنك ترغب في وصف كوكبنا: الأرض. هناك عدد من الأشياء التي يمكننا اختيار النظر إليها ودراستها. على سبيل المثال، يمكننا أن نقرر النظر فقط إلى سطح الأرض، و طرح أسئلة حول التضاريس في كل نقطة على الكرة الأرضية. في لحظة، يمكنك البدء في التفكير في بعض الأشياء التي قد ترغب في معرفتها. وتشمل هذه:

• أين ننظر، الآن، من حيث المكان؟
• متى تكون اللحظة الزمنية التي نهتم بها؟
• ما هو ارتفاعنا فوق “مستوى سطح البحر” لسطح الأرض؟
• إذا وضعت كرة، فأي اتجاه ستتدحرج، وكم ستكون سرعتها في التدهور على ذلك المنحدر؟
• هل هناك أي إجهاد أو انفعال على الأرض في تلك النقطة؟
• إذا وضعت كمية كبيرة من الماء، كيف سيتدفق الماء؟ أي طريق سيسلك وكم ستكون سرعته؟ هل سيتطور دوامات أو دوامة في أي مكان؟

إن الأرض نفسها ليست سوى جسم واحد نتأمله، ولكن التفكير في سطح كوكبنا يُعطينا طريقة رائعة للتفكير فيما هو مجال، بالإضافة إلى الأنواع المختلفة من المجالات التي تهم العلم.

يبلغ قطر الأرض عند خط الاستواء 12,756 كم، بينما يبلغ عند القطبين 12,714 كم فقط. أنت أقرب بـ 21 كيلومتراً إلى مركز الأرض عندما تقف عند القطب الشمالي مقارنةً بخط الاستواء. ويعود هذا الاختلاف إلى حد كبير إلى دوران الأرض المحوري. وهناك أيضاً سمات أخرى مثل الجبال والوديان والتلال، وأكثر من ذلك مُثبّت فوق هذا الشكل الكروي المفلطح بشكل عام.

لنبدأ بسؤال الارتفاع. لو كانت الأرض مثالية، ناعمة، ولم تكن تدور، لكانت ستشكل كرةً دقيقة. ولأن الأرض تدور، فإن هذا الشكل ينضغط عند القطبين وينتفخ في المنتصف، مشكلاً شكلاً يُعرف باسم الكروي المفلطح. ومع ذلك، هناك ارتفاعات وانخفاضات على طول السطح، مع امتلاء المحيطات والبحار والبحيرات والأنهار لبعض الأعماق العميقة بالمياه.

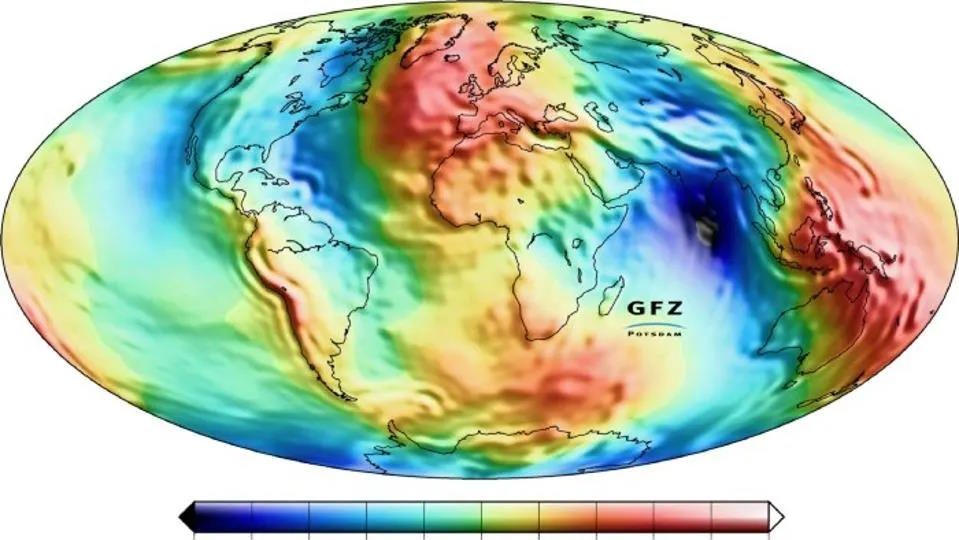
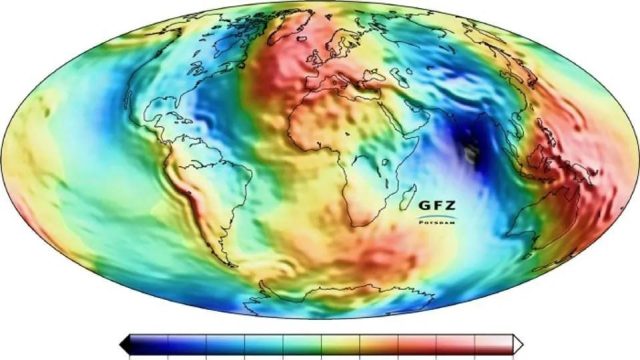
في كل مكان على السطح، إذن، يمكننا طرح سؤال مثل، “ما هو ارتفاعنا فوق مستوى سطح البحر؟” حيث مستوى سطح البحر هو الارتفاع الذي ستغطي فيه المحيطات كل نقطة على الأرض لو لم تكن هناك كتل أرضية ترتفع فوقه. لذا، إذا أردت وصف “ما هو ارتفاعك فوق مستوى سطح البحر” في كل نقطة على سطح الأرض، كيف ستفعل ذلك؟

هذه هي الحالة بالضبط التي تستدعي استخدام حقل قياسي.

يُظهر هذا الخريطة الطبوغرافية أنَّ الجزء الشمالي من سطح المريخ (40%) يقع على ارتفاع أقل بحوالي 5 كيلومترات من بقية الكوكب. وقد تكون هذه الخاصية الضخمة، المعروفة باسم حوض بورياليس، قد تشكلت نتيجة اصطدام كبير ربما أدى إلى تناثر ما يكفي من الحطام لتشكيل العديد من الأقمار.

إنّ الحقل القياسي، بصراحة، هو أبسط أنواع الحقول التي يمكنك الحصول عليها. فما يقوله هو أنه إذا أعطيت القيم التي تخبرك بـ”أين” و”متى” أنت – أين أنت في الفضاء ومتى أنت في الزمن – فسوف يعطيك الحقل القياسي قيمة واحدة فقط تصف “كمية” الشيء الذي تحاول قياسه. وإذا كان هذا الشيء الذي تسأل عنه هو “الارتفاع عن مستوى سطح البحر”، فيمكن للحقل القياسي أن يخبرك بهذا الارتفاع. ليس فقط في المتوسط، أو على السطح كله، بل في كل نقطة. وإذا كان ارتفاع الأرض شيئًا يتغير مع مرور الوقت (وعلى مدى فترات زمنية طويلة، فهو كذلك)، فيمكن للحقل القياسي أن يلتقط ذلك أيضًا.

لكن هذا الحقل القياسي لن يخبرك بكل ما ترغب في معرفته عن سطح الأرض. إنه فقط يخبرك “بما هي قيمة الشيء الذي أسأل عنه في أي نقطة في الفضاء و/أو في أي لحظة زمنية”. وإذا كنت تريد، بدلاً من ذلك، معرفة إجابة بعض الأسئلة الأخرى مثل، “في أي اتجاه ستتدفق المياه على هذا السطح؟” فإن الحقل القياسي لا يكفي.

لهذا، ستحتاج إلى خريطة منحدر بدلاً من ذلك، وهذا ليس حقلًا قياسيًا، بل هو حقل متجه.

يُظهر التضاريس الموضحة هنا، والتي تُمثل جبل شارب على سطح المريخ من خلال مركبة كيوريوسيتي الجوالة، العديد من الخصائص: الارتفاع والانحدار، على سبيل المثال، في كل نقطة. إن مجرد بيان الارتفاع في كل نقطة يُمثل كمية قياسية؛ أما بيان الانحدار في كل نقطة فهو كمية متجهة.

إذن، ما هو المجال المتجه، وما هو اختلافُه عن المجال القياسي؟

لا يخبرك حقل المتجهات فقط بقيمة شيء ما في كل نقطة من نقاط المكان والزمان، بل يخبرك بقيمة واتجاه تلك القيمة أيضًا بمعنى ما. سيتدفق النهر دائمًا، في أي نقطة، بسرعة معينة، لكن السرعة وحدها لا تكفي لوصف حركته بالكامل. يتدفق النهر أيضًا بطريقة معينة باتجاه معين: نحتاج إلى معرفة الاتجاه الذي يتجه إليه، وليس فقط مدى سرعته.

هناك شيء إضافي يمكننا فعله باستخدام حقل متجه لا يمكننا فعله باستخدام حقل قياسي: يمكن أن يؤدي حقل متجه إلى “دوران“، والذي يصف كيف تتحرك الأجسام حول نقطة معينة في الفضاء. في الرياضيات، يكون دوران الحقل القياسي دائمًا صفرًا، لذلك إذا استخدمنا فقط الحقول القياسية، فلن يكون لدينا أبدًا دوامة، أو دوامة مائية، أو إعصار، أو حركة تصف الدوران في دائرة. إذا وجهت إبهامك في اتجاه واحد ونظرت إلى كيفية رغبة أصابعك في الالتفاف حول يدك، فإن حركة الالتفاف التي ستحاول القيام بها هي إحدى طرق تصور الدوران.

يوضح هذا الرسم التوضيحي حقل متجه ثنائي الأبعاد منتظم يمثل الدوامة. يمكن الحصول على طبيعة الدوامة في اتجاه عقارب الساعة بطريقتين: إما بتوجيه كمية أساسية ذات يد يسارية مثل إبهام يدك اليسرى نحوك، حيث تتجعد أصابعك في اتجاه عقارب الساعة، أو بتوجيه كمية ذات يد يمنى، مثل إبهام يدك اليمنى، بعيدًا عنك.

في عالمنا الملموس الواقعي، يمكن أن تصلنا الحقول القياسية إلى حد بعيد، لكنها لا تستطيع أن تحقق لنا أي شيء نتخيله. ولتفسير الحركة، نحتاج إلى معرفة اتجاه الأشياء، وهذا يعني مجالاً متجهًا. ولتفسير القوى، وبالتالي، كيف تتغير الحركة بمرور الوقت، لا نحتاج فقط إلى مقدار القوة، بل أيضًا إلى اتجاه تلك القوة. بالنسبة للحركات الدورانية، مثل دوران الأشياء أو دورانها حول أجسام أخرى، نحتاج أيضًا إلى حقول متجهة؛ هل تتجعد الأشياء بالطريقة التي تتجعد بها أصابعك حول يدك اليمنى أم اليسرى؟

تأمّل في جميع السمات المختلفة التي قد يمتلكها جسم ما والتي قد ترغب في معرفتها أو قياسها أو استخدامها للتنبؤ بنتيجة نظام مُعدّ بطريقة معينة. فيمكن وصف جميعها تقريبًا بشكل كامل إما بمجال قياسيّ (معرفة المقدار فقط كافية) أو بمجال متجهيّ (حيث يكون المقدار والاتجاه الذي يشير إليه مهمًّا).

• الكتلة كمية قياسية.
• السرعة كمية قياسية.
• الارتفاع كمية قياسية.
• المسافة كمية قياسية.
• الزمن المنقضي كمية قياسية.
• الميل متجه.
• “الاتجاه” متجه.
• العزم متجه.
• والقوة متجهة.

حسنًا، القوة متجهة في الغالب؛ هناك شيء بسيط آخر يجب مراعاته في المثال الأخير.

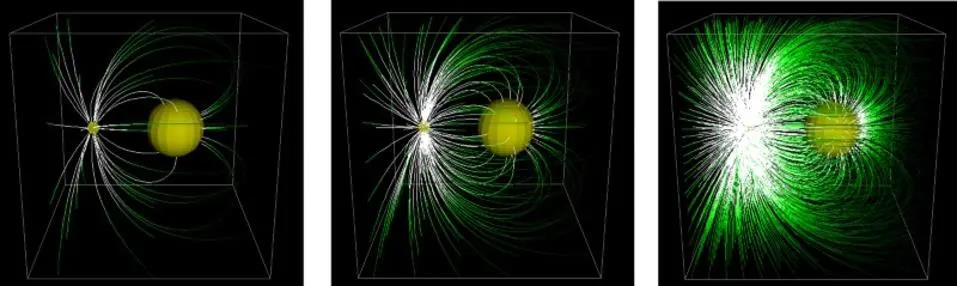
تُوصَفُ الحقولُ الكهربائيّةُ والقُوَى الكهربائيّةُ جيّداً بالمتجهات، حيثُ تملِكُ كلٌّ منهما مقداراً واتّجاهًا، دونَ أيّ خصائصَ أُخرى مُرتبطةٍ بها. أمّا إذا كانت الأشياءُ تملِكُ مقداراً فقط، مثل الجهد، فيمكن وصفُها بمجالٍ قياسيّ. ويمكن أن تتطلّب الكياناتُ الأكثر تعقيداً، مثل الجاذبيّة، معاملاتٍ إضافيّة، مما يستلزم استخدام مجالٍ مُوتِّر بدلاً من ذلك.

في نظر نيوتن، القوّةُ دائماً متّجهة. لها شدّةٌ وتسيرُ في اتّجاهٍ مُعيّن، وهذا يكفي لوصفها وصفاً كاملاً. بين جسمين مشحونين، تلك القوّةُ متّجهة. داخل نواة الذرّة، تلك القوى – بين البروتونات والنيوترونات وحتى داخل البروتون نفسه – كلّها متجهات.

لكن في نظر آينشتاين، عندما يتعلق الأمر بأشهر القوى على الإطلاق (القوة التي تحدث بين جميع الأجسام الضخمة، ولكنها تحتوي على أجزاء كثيرة من الكلمات لاستخدامها هنا)، فإن القوة ليست كمية قياسية ولا كمية متجهة، بل تتطلب شيئًا أكثر تعقيدًا لوصفها: وهو موتر.

إذن ما هو الموتر؟

تخيل جسمًا صلبًا مثل عمود إسمنتي. لديك هذا العمود، وأنت تراقبه، وتُعرّضه للعديد من العوامل الواقعية. فهو يصبح ساخنًا وباردًا. ويوضع عليه وزن ثم يُزال. ويدفعه الناس، ويسحبونه، أو يستندون إليه. والكتل المحيطة به جميعًا تسحب (أو تدفع) عليه. لو استطعتَ رسم خريطة لجميع القوى المختلفة التي تؤثر داخل العمود، بما في ذلك أشياء مثل الإجهادات والشدود، لوجدت أنها لا تختلف فقط مع الزمن وفي اتجاهاتها، بل إن المجال المتجهي وحده لا يكفي لوصفها. بدلاً من ذلك، ستحتاج إلى شيء أوسع نطاقًا، يمكنه أن يتضمن أشياءً لا تستطيع المتجهات والكميات القياسية تمثيلها. هنا تحتاج إلى مُوتر.

تُعدُّ سلطة الجيلي، كما هو موضح في هذه الصورة الملتقطة في أحد محلات السوبر ماركت بالولايات المتحدة، مثالًا على بنية تتحول كمُوتر. فإذا ثَقَبْتَ قالب جيلي، ستشاهد المادة الهلامية وهي تتذبذب وتتشوه نتيجة لذلك. لا يمكن وصف القوى والتشوهات الداخلية داخل قالب الجيلي نفسه باستخدام حقل قياسي أو حقل متجه، بل تتطلب شيئًا أكثر تعقيدًا: وهو حقل موتر.

إذا دفعت شيئًا ما في اتجاه محدد، فمن المتوقع أن يتجه القوة في نفس الاتجاه: على طول ذلك المحور المميز الذي دفعته. ولكن في بعض الأحيان – ويمكنك دفع قالب جيلي متجمد إذا أردت رؤية التأثير بنفسك – فإن قوة بدء تشير إلى اتجاه واحد يمكن أن تخلق قوى داخل الجسم (أو على جسم) تشير على طول محاور مختلفة عن الفعل الأولي الذي بدأ كل شيء. هذا يخلق قوى على طول خطوط لا يمكنك تفسيرها إذا كنت تعمل فقط مع الحقول القياسية أو المتجهة.

كان هذا هو مفتاح فكرة أينشتاين العظيمة. إذا استطعت، من أي وجهة نظر تختارها، أن تخبرنا:

• أين توجد جميع الكتل، وال فوتونات، وغيرها من الكميات،
• وما هي قيم كتلتها وقيمها الشبيهة بالكتلة،
• وكيف يتم وضعها،
• وكيف تتحرك في أي نقطة زمنية واحدة،

حينئذٍ، تستطيع نظرية آينشتاين أن تخبرك، في كل نقطة في المكان والزمان، كيف سينحني الفضاء، وكيف سيخبر الفضاء المادة والفوتونات وكل كم آخر كيف يتحرك.

إنّ إلقاء نظرة متحركة على كيفية استجابة الزمكان عندما تتحرك كتلة خلاله يساعد على إبراز بالضبط كيف، نوعياً، ليس مجرد قطعة قماش. بل إنّ كل الفضاء ثلاثي الأبعاد نفسه ينحني بوجود وخصائص المادة والطاقة داخل الكون. ستؤدي الكتل المتعددة التي تدور حول بعضها البعض إلى انبعاث موجات جاذبية.

هذه النظرية — وهي أعظم إنجاز علمي في حياة أينشتاين — نظرية تنسورية بحتة. لا يوجد جزء قياسي؛ ولا يوجد جزء متجه. في الواقع، هناك حدود صارمة للغاية على مقدار ما يمكن أن يساهم به جزء “قياسي” أو “متجه” في انحناء الزمكان. إذا أردنا الحصول على الكون الذي نعرفه ونلاحظه، فلا يمكن أن يكون هناك أجزاء قياسية أو متجهة للقانون الذي يحكم الزمكان.

وهذه هي إحدى المشاكل الكبرى في نظرية الأوتار. فإن نظرية الأوتار لا تعطيك فضاءً ثلاثي الأبعاد (أو زمكان رباعي الأبعاد)، بل ستة أبعاد إضافية يجب التخلص منها. إنها لا تعطيك نظرية تنسورية تخبرك كيف تحني الكتلة الزمكان، بل نظرية تحتوي على قياسيات وموترات، ويجب عليك تطهير النظرية من جميع القياسيات. ببساطة، إنها تعطيك “مواد إضافية” لكوننا لا يوجد لها وجود في كوننا.

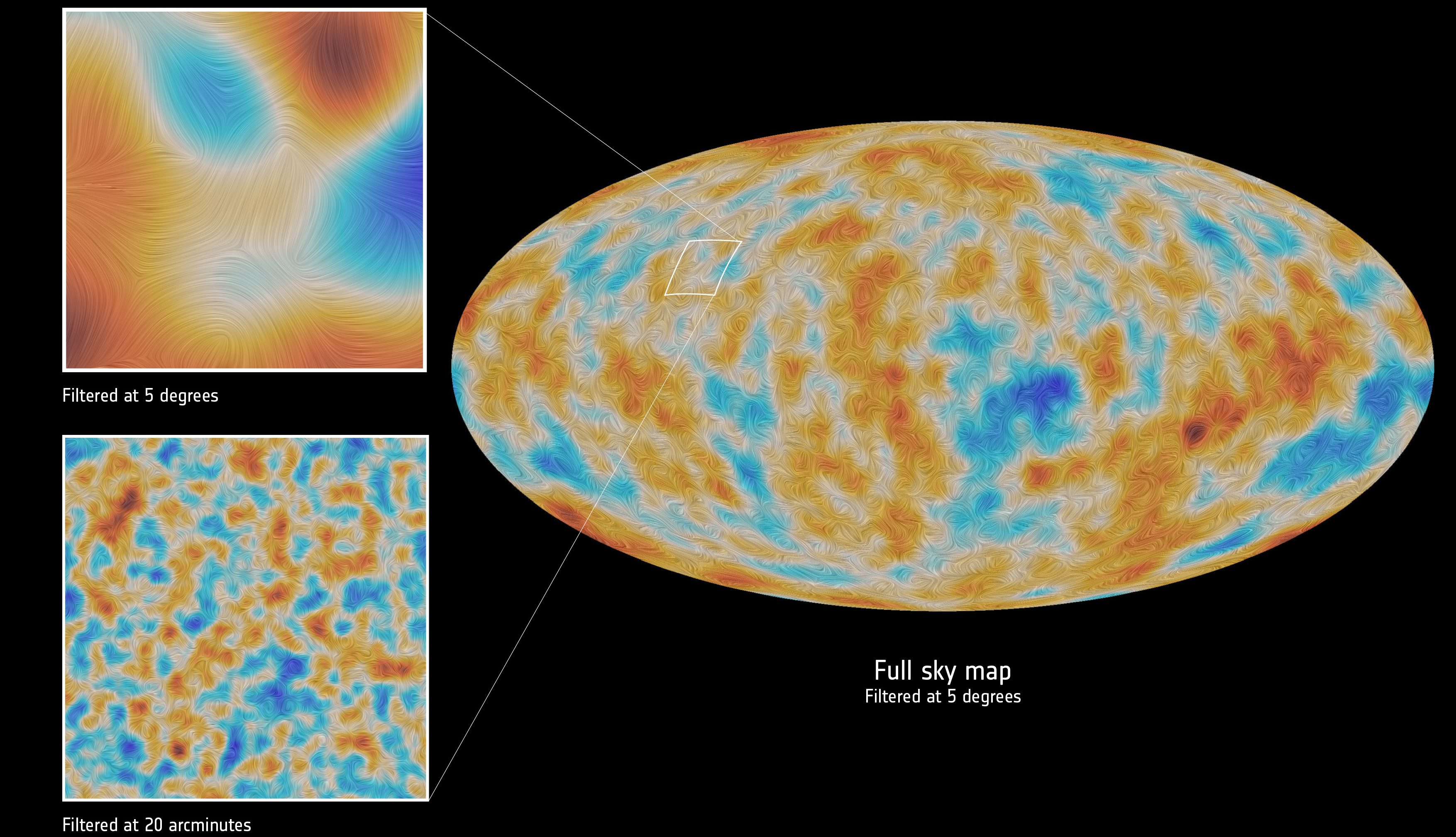
يأتي أحد أصعب الاختبارات من مشروع ليغو، الذي رصد تموجات في نسيج الزمكان من أكثر من 50 حدثًا حتى اليوم. وتُظهر طريقة تشويهها لنسيج الفضاء طبيعةً تنسوريةً بحتة، مع هامش ضئيل جدًا لوجود أجزاء قياسية أو متجهة؛ فقد أصبحت القيود شديدة للغاية.

عندما تمر موجة جاذبية عبر موقع في الفضاء، فإنها تسبب تمددًا وانضغاطًا في أوقات متناوبة وفي اتجاهات متناوبة، مما يتسبب في تغير أطوال أذرع الليزر في اتجاهات متعامدة بشكل متبادل. ومن خلال استغلال هذا التغيير الفيزيائي، تم تطوير كاشفات موجات الجاذبية الناجحة مثل ليغو وفيرغو.

باختصار، لا يمكن للحقل القياسي أن يوفر لك إلا “كمية” من شيء ما، ولكنه يمكن أن يوفرها لك في كل نقطة في الفضاء في أي وقت تختاره. إذا أردت إضافة شيء أكثر، مثل اتجاه كمية من شيء ما، فأنت بحاجة إلى الترقية إلى حقل متجه. وإذا كان لديك شيء أكثر تعقيدًا، مثل:

• الفضاء المنحني،
• الإجهادات والانفعال،
• أو التأثيرات التي تشير على طول عناوين مختلفة عن القوة التي أنتجتها،

حتى الحقل المتجه لا يمكنه التقاطها جميعًا. لذلك، فأنت بحاجة إلى حقل موتر، مثل نظرية أينشتاين لكيفية انحناء الكتلة والمادة وأكثر من ذلك للزمكان.

(من الكتب التي أحبها والتي تتعمق في التفاصيل الدقيقة حول الفرق بين الكميات القياسية والمتجهات، وكيف تسمح لنا باستنتاج خصائص مختلفة من عالمنا الحقيقي، كتاب الاختلاف والتدرج والدوامة وكل ذلك؛ وإذا كنت قد واجهت صعوبة في الرياضيات المتقدمة في الكلية، فقد يساعدك هذا الكتاب على توضيح بعض الأفكار المعقدة.)

إن المجال القياسي هو مجرد مجال يُعيّن له قيمة – أو مقدار – ولا شيء آخر. وإذا أردت معرفة أي شيء آخر، حتى أبسط شيء مثل اتجاه شيء ما، فإن الكمية القياسية ببساطة لن تفعل ذلك. قد تكون هناك كميات قياسية إضافية موجودة هناك في شكل حقول أو كميات لم نلتقِ بها بعد، ولكن بقدر ما نعرف، لا يوجد منها ما هو جزء من نظرية آينشتاين. وإيجاد السبب في ذلك هو أحد التحديات التي لم تتمكن نظرية الأوتار من تجاوزها حتى الآن.

إيثان في إجازة هذا الأسبوع. نرجو أن تستمتعوا بـ هذه المقالة من أرشيف “يبدأ بانفجار”!