”

هناك سؤال وجودي هائل تساءلنا عنه منذ أن أدركنا لأول مرة أن الكون يخضع بالفعل لقوانين فيزيائية: لماذا كوننا على ما هو عليه بالضبط، بدلاً من أي طريقة أخرى يمكن أن نتخيلها؟ لا يوجد سوى ثلاثة أشياء تجعله كذلك:

• قوانين الطبيعة نفسها،
• الثوابت الأساسية التي تحكم الواقع،
• والشروط الأولية التي وُلد بها كوننا.

لو كان لكوننا قوانين طبيعة مختلفة، لكانت كل الرهانات باطلة؛ لكان الكون مختلفًا بشكل هائل بأي طريقة يمكن أن تتخيلها. ربما تتحلل البروتونات، وربما لا تكون الكميات الأساسية مثل كتل الجسيمات ثابتة، وقد تتغير قوى أي قوى أساسية بشكل مفاجئ في أي لحظة.

لو اختلفت الظروف الأولية لكوننا، لبقيت قصة الكون الكونية كما هي من حيث الخطوط العريضة، ولكن ستختلف التفاصيل بين ذلك الكون الافتراضي وكوننا. ولكن بالنسبة للثوابت الأساسية، ستكون بعض التغييرات عميقة، بينما ستكون أخرى بالكاد ملحوظة. في كوننا، للثوابت القيم الصريحة التي تمتلكها، وهذا المزيج المحدد ينتج الكون الصديق للحياة الذي نسكنه. أحد هذه الثوابت الأساسية يُعرف بثابت البنية الدقيقة، وقيمته التقريبية (1/137) تظهر في الحسابات التي تهم مجموعة كاملة من الظواهر، على المستويين دون الذري والكوني على حد سواء.

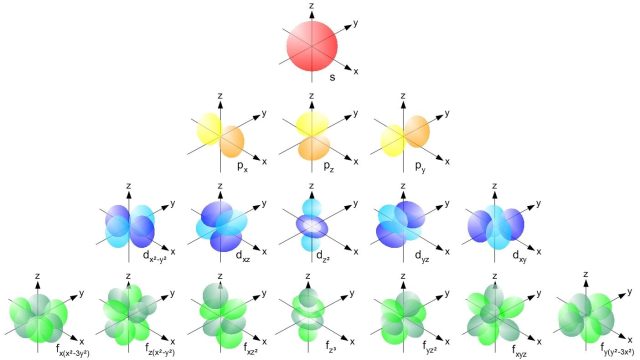
تبدأ قصتنا مع اللبنات البسيطة للمادة التي يتكون منها الكون: الجسيمات الأساسية للنموذج القياسي.

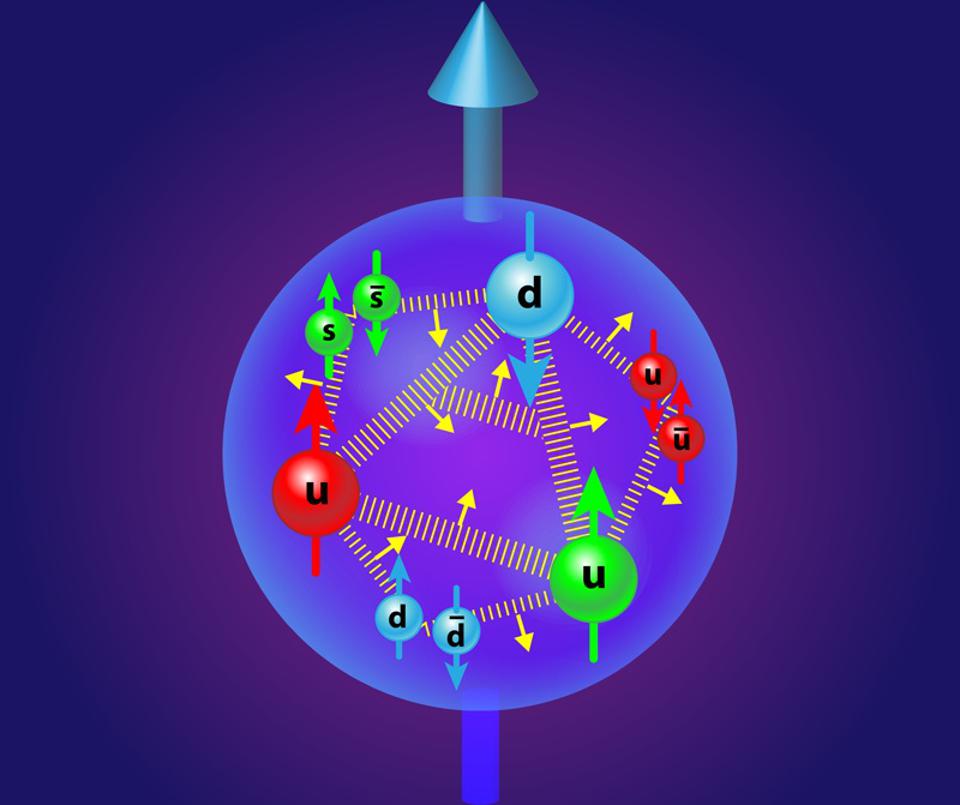
يُظهر نموذجُ بنيةِ البروتون، مع حقوله المصاحبة، كيف أنَّهُ على الرغم من تكوينه من كواركات وجلوونات نقطية، إلا أنَّ له حجمًا محدودًا وملموسًا ينشأ من التفاعل بين القوى والحقول الكمية بداخله. والبروتون نفسه جسيمٌ كميٌّ مركب، وليس أساسيًا. أما الكواركات والجلوونات الموجودة بداخله، بالإضافة إلى الإلكترونات التي تدور حول نوى الذرات، يُعتقد أنها أساسيةٌ حقًا وغير قابلةٍ للانقسام.

يتكون كوننا، إذا قمنا بتقسيمه إلى أصغر مكوناته، من جسيمات النموذج القياسي. ترتبط الكواركات والغلونات، وهما نوعان من هذه الجسيمات، معًا لتشكيل حالات مرتبطة مثل البروتون والنيوترون، التي ترتبط بدورها معًا لتشكيل نوى الذرات. والإلكترونات، وهي نوع آخر من الجسيمات الأساسية، هي أخفّ الليبتونات المشحونة. وعندما ترتبط الإلكترونات ونوى الذرات معًا، فإنها تشكل الذرات: وهي اللبنات الأساسية للمادة العادية التي تشكل كل شيء في تجربتنا اليومية.

قبل أن يدرك البشر حتى بنية الذرات، كنا قد حددنا العديد من خصائصها. في القرن التاسع عشر، اكتشفنا أن الشحنة الكهربائية للنواة تحدد الخصائص الكيميائية للذرة، واكتشفنا أن كل ذرة لها طيفها الفريد من الخطوط التي يمكن أن تنبعث منها وتمتصها. تجريبياً، كان الدليل على كون كمي منفصل معروفًا قبل وقت طويل من وضع النظريين كل شيء معًا.

يُظهر طيف الضوء المرئي للشمس، والذي يساعدنا على فهم درجة حرارتها وتأينها، بالإضافة إلى وفرة العناصر الموجودة. تمثل الخطوط الطويلة السميكة الهيدروجين والهيليوم، ولكن كل خط آخر ينتمي إلى عنصر ثقيل. العديد من خطوط الامتصاص المعروضة هنا قريبة جدًا من بعضها البعض، مما يدل على وجود بنية دقيقة، والتي يمكن أن تقسم مستويين طاقة متدهورين إلى مستويات متقاربة ولكنها مميزة.

في عام 1912، اقترح نيلز بور نموذجه الشهير للذرة، حيث تدور الإلكترونات حول النواة الذرية مثلما تدور الكواكب حول الشمس. لكن الفرق الكبير بين نموذج بور ونظامنا الشمسي هو أن هناك حالات معينة فقط مسموح بها للذرة، بينما يمكن للكواكب أن تدور بأي تركيبة من السرعة ونصف القطر تؤدي إلى مدار مستقر.

أدرك بور أن الإلكترون والنواة صغيران جدًا، ولهما شحنتان متضادتان، وعلم أن النواة تحتوي على معظم الكتلة تقريبًا. وكان إسهامه الرائد هو فهم أن الإلكترونات لا يمكنها إلا أن تشغل مستويات طاقة معينة، والتي أطلق عليها اسم “المدارات الذرية”. لا يمكن للإلكترون أن يدور حول النواة إلا بخصائص معينة، مما يؤدي إلى خطوط الامتصاص والانبعاث المميزة لكل ذرة على حدة.

عندما تعاد اتحاد الإلكترونات الحرة مع نوى الهيدروجين، تتساقط الإلكترونات عبر مستويات الطاقة، مُنطلقة فوتونات أثناء سقوطها. ولكي تتكون ذرات مستقرة ومتعادلة في الكون المبكر، يجب أن تصل إلى الحالة الأرضية دون إنتاج فوتون فوق بنفسجي مُؤين محتمل. يوفر نموذج بوهر للذرة البنية الخشنة (أو التقريبية) لمستويات الطاقة، ولكن هذا كان غير كافٍ بالفعل لوصف ما شوهد قبل عقود.

فشل هذا النموذج، برغم براعته وذكائه، على الفور في إعادة إنتاج نتائج التجارب التي أجريت منذ عقود في القرن التاسع عشر. ففي عام 1887، حدد مايكلسون ومورلي خصائص الانبعاث والامتصاص الذري للهيدروجين، ولم تتطابق تمامًا مع تنبؤات ذرة بور.

لقد قام نفس العالمان اللذان حصلا على نتيجة عدم وجود فرق في سرعة الضوء سواء تحرك مع حركة الأرض أو عكسها أو بشكل عمودي عليها، بقياس خطوط طيف الهيدروجين بدقة أكبر من أي شخص آخر من قبل. وبينما اقترب نموذج بور من هذه النتائج، أظهرت نتائج مايكلسون ومورلي تحولات طفيفة وحالات طاقة إضافية انحرفت قليلاً ولكن بشكلٍ كبير عن تنبؤات بور. على وجه الخصوص، كانت هناك بعض مستويات الطاقة التي بدت وكأنها تنقسم إلى قسمين، بينما تنبأ نموذج بور بواحد فقط.

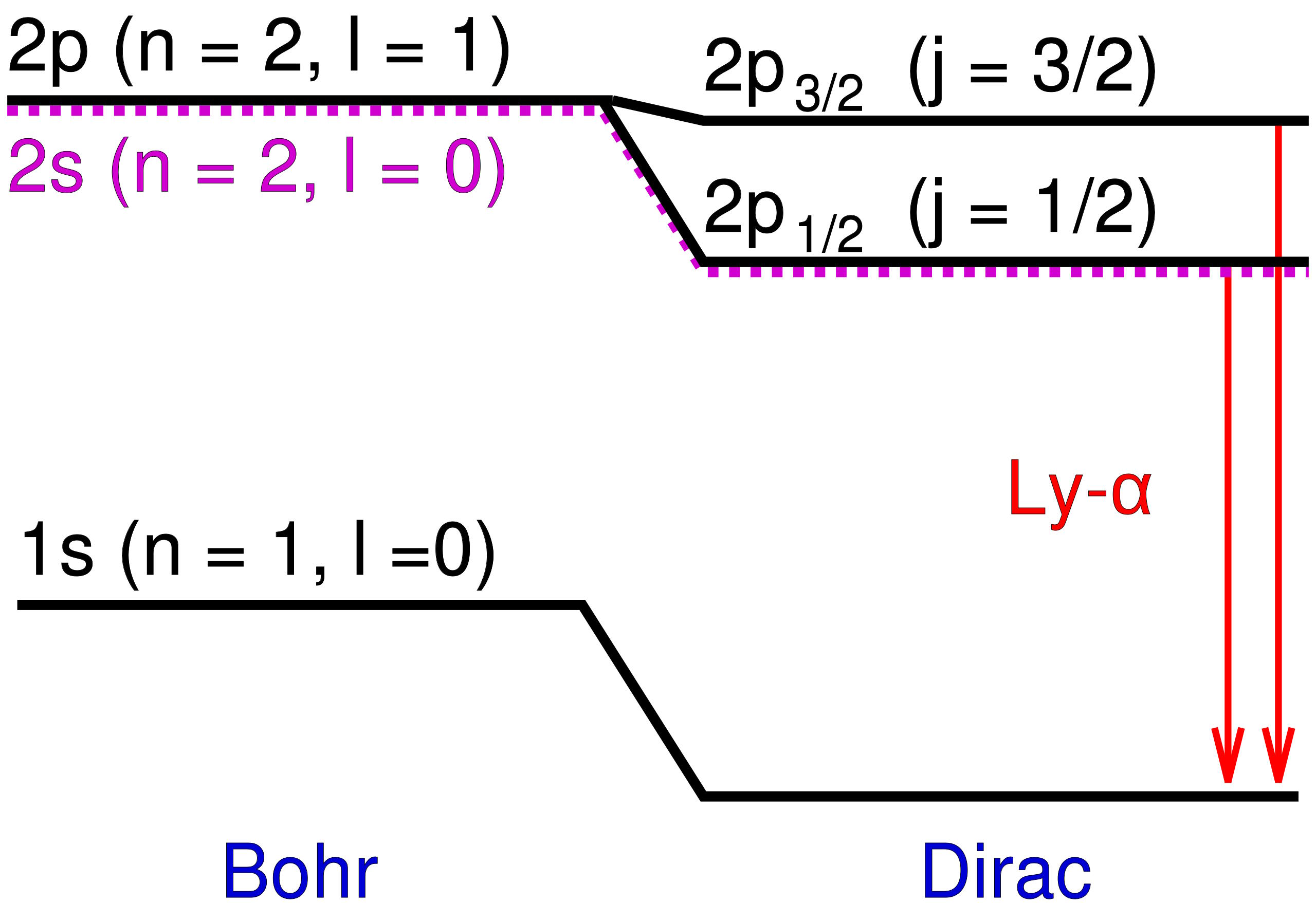
في نموذج بور لذرة الهيدروجين، تساهم فقط الزخم الزاوي المداري للإلكترون الشبيه بالنقطة في مستويات الطاقة. إن إضافة التأثيرات النسبية وتأثيرات الدوران لا تسبب فقط تحولًا في مستويات الطاقة هذه، بل تسبب أيضًا انقسام المستويات المتدهورة إلى حالات متعددة، مما يكشف عن البنية الدقيقة للمادة فوق البنية الخشنة التي تنبأ بها بور.

لقد كانت تلك المستويات الإضافية للطاقة، التي كانت قريبة جدًا من بعضها البعض وقريبة أيضًا من تنبؤات بور، أول دليل على ما نسميه الآن البنية الدقيقة للذرات. وقد نجح نموذج بور، الذي قام بشكل مبسط بنمذجة الإلكترونات كجسيمات مشحونة عديمة الدوران تدور حول النواة بسرعات أقل بكثير من سرعة الضوء، في تفسير البنية الخشنة للذرات، ولكن ليس هذه البنية الدقيقة الإضافية.

وهذا يتطلب تقدماً آخر، جاء في عام 1916 عندما توصل الفيزيائي أرنولد سومرفيلد إلى إدراك. إذا قمت بنمذجة ذرة الهيدروجين كما فعل بور، وقارنت نسبة سرعة إلكترون الحالة الأرضية بسرعة الضوء، فستحصل على قيمة محددة جدًا، أطلق عليها سومرفيلد اسم α: ثابت البنية الدقيقة. هذا الثابت، بمجرد دمجه بشكل صحيح في معادلات بور، أصبح قادرًا على حساب فرق الطاقة بدقة بين تنبؤات البنية الخشنة والدقيقة.

لا يُظهر مصدر الديوتيريوم المُبرد فائق التبريد، كما هو موضح هنا، مستويات منفصلة ببساطة، بل هامشًا يقع فوق نمط التداخل البنّاء/الهدّام القياسي. ويُعزى هذا التأثير الهامشي الإضافي إلى البنية الدقيقة للمادة.

من حيث الثوابت الأخرى المعروفة في ذلك الوقت، α = e²/(4πε_0)ħc، حيث:

• e هي شحنة الإلكترون،
• ε_0 هو الثابت الكهرومغناطيسي لنفاذية الفراغ،
• ħ هو ثابت بلانك،
• وc هي سرعة الضوء.

على عكس هذه الثوابت الأخرى، التي ترتبط بها وحدات، فإن α ثابت عديم الأبعاد حقًا، وهذا يعني أنه مجرد عدد نقي، بدون أي وحدات مرتبطة به على الإطلاق. في حين أن سرعة الضوء قد تختلف إذا قمت بقياسها بالأمتار في الثانية، أو الأقدام في السنة، أو الأميال في الساعة، أو أي وحدة أخرى، فإن قيمة α تبقى ثابتة دائمًا. ولهذا السبب، يُعتبر أحد الثوابت الأساسية التي تصف كوننا.

مستويات الطاقة ووظائف الموجة الإلكترونية التي تتوافق مع حالات مختلفة داخل ذرة الهيدروجين، على الرغم من أن التكوينات متشابهة للغاية لجميع الذرات. تُكمم مستويات الطاقة بمضاعفات ثابت بلانك، ولكن أحجام المدارات والذرات يحددها مستوى الطاقة الأرضية وكتلة الإلكترون. قد تكون التأثيرات الإضافية دقيقة، ولكنها تُحرك مستويات الطاقة بطرق قابلة للقياس والكمّ.

لا يمكن تفسير مستويات طاقة الذرة بشكل صحيح دون تضمين هذه التأثيرات الدقيقة للبنية، وهي حقيقة عادت للظهور بعد عقد من زمن بور عندما ظهرت معادلة شرودنجر. وكما فشل نموذج بور في إعادة إنتاج مستويات طاقة ذرة الهيدروجين بشكل صحيح، فشلت معادلة شرودنجر أيضًا. وقد سرعان ما تم اكتشاف ثلاثة أسباب لذلك.

1. إن معادلة شرودنجر غير نسبية أساسًا، ولكن الإلكترونات والجسيمات الكمية الأخرى يمكن أن تتحرك بسرعة قريبة من سرعة الضوء، ويجب تضمين هذا التأثير.
2. لا تدور الإلكترونات حول الذرات ببساطة، بل تمتلك أيضًا زخمًا زاويًا داخليًا متأصلًا فيها: الدوران، بقيمة ħ/2، والتي يمكن أن تكون محاذاة أو مضادة للمحاذاة مع باقي الزخم الزاوي للذرة.
3. تُظهر الإلكترونات أيضًا مجموعة متأصلة من التقلبات الكمية لحركتها، والمعروفة باسم زيتربيفيج؛ وهذا يساهم أيضًا في البنية الدقيقة للذرات.

عندما تتضمن كل هذه التأثيرات، يمكنك إعادة إنتاج كل من البنية الكلية والدقيقة للمادة بنجاح.

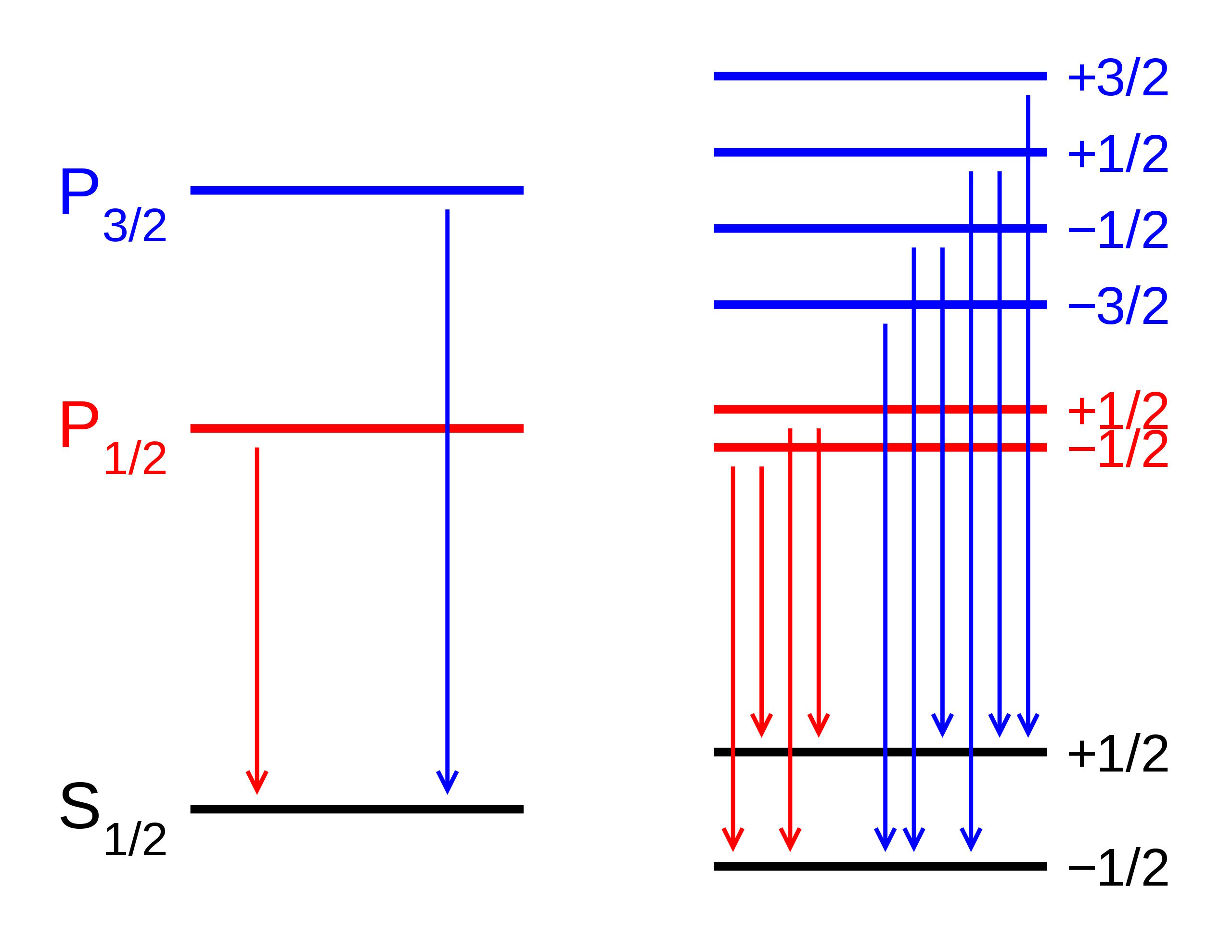
في غياب المجال المغناطيسي، تكون مستويات الطاقة للحالات المختلفة داخل المدار الذري متطابقة (L). أما إذا تم تطبيق مجال مغناطيسي (R)، فإن الحالات تنقسم وفقًا لتأثير زيمان. نرى هنا انقسام زيمان في انتقال ثنائي P-S. تحدث أنواع أخرى من الانقسام بسبب التفاعلات بين العزم المغزلي والمداري، والآثار النسبية، والتفاعلات مع العزم المغزلي النووي، مما يؤدي إلى البنية الدقيقة وفائقة الدقة للمادة.

يُعزى ضآلة هذه التصحيحات إلى صغر قيمة ثابت البنية الدقيقة، α، أيضًا. ووفقًا لأفضل قياساتنا الحديثة، فإن قيمة α = 0.007297352569، حيث الرقم الأخير فقط هو غير مؤكد. وهذا قريب جدًا من أن يكون رقمًا دقيقًا: α = 1/137. وقد اعتُبر ذات مرة من الممكن تفسير هذا الرقم الدقيق بطريقة ما، لكن البحوث النظرية والتجريبية الأفضل أظهرت أن العلاقة غير دقيقة، وأن α = 1/137.0359991، حيث الرقم الأخير فقط هو غير مؤكد مرة أخرى.

ينشأ خط الهيدروجين الذي يبلغ طوله 21 سنتيمتراً عندما ينقلب ذرّة هيدروجين تحتوي على مزيج من البروتون/الإلكترون ذي دوران متوافق (أعلى) ليكون ذي دوران غير متوافق (أسفل)، مُنبعثة فوتوناً واحداً بطول موجي مميز للغاية. يمثل التكوين ذو الدوران المعاكس في مستوى الطاقة n=1 الحالة الأرضية للهيدروجين، لكن طاقة نقطة الصفر الخاصة به قيمة منتهية غير صفرية. يُعد هذا الانتقال جزءاً من البنية الدقيقة الفائقة للمادة، متجاوزاً حتى البنية الدقيقة التي نشهدها بشكل أكثر شيوعاً.

لكن حتى مع الأخذ في الاعتبار كل هذه التأثيرات، لا نحصل على كل شيء يتعلق بالذرات. فلا يوجد فقط البنية الخشنة (من مدارات الإلكترونات حول النواة) والبنية الدقيقة (من التأثيرات النسبية، ودوران الإلكترون، وتذبذبات الإلكترون الكمية)، بل هناك أيضًا البنية فائقة الدقة: وهي تفاعل الإلكترون مع دوران النواة. فانتقال انعكاس الدوران في ذرة الهيدروجين، على سبيل المثال، هو أضيق خط طيفي معروف في الفيزياء، وهو ناتج عن هذا التأثير فائق الدقة الذي يتجاوز حتى البنية الدقيقة.

يوفر ضوء الكوازارات البعيدة جدًا مختبرات كونية لقياس سحب الغاز التي تصادفها في طريقها، بالإضافة إلى الوسط بين المجرات الذي يحتوي على بلازما دافئة وساخنة خارج العناقيد والمجرات والخيوط. ولأن الخصائص الدقيقة لخطوط الانبعاث أو الامتصاص تعتمد على ثابت البنية الدقيقة، فإن هذه إحدى أفضل الطرق للتحقيق في الكون بحثًا عن تغيرات زمنية أو مكانية في ثابت البنية الدقيقة.

لكن ثابت البنية الدقيقة، α، يحظى باهتمام بالغ في الفيزياء. وقد بحث البعض فيما إذا كان هذا الثابت مثاليًا أم لا. وقد أشارت قياسات متنوعة، في نقاط مختلفة من تاريخنا العلمي، إلى أن α قد يتغير مع الزمن أو من مكان إلى آخر في الكون. وقد أشارت قياسات الخطوط الطيفية للهيدروجين والديوتيريوم، في بعض الحالات، إلى أن α ربما يتغير بنسبة ~0.0001٪ عبر المكان أو الزمن.

ومع ذلك، فإن هذه النتائج الأولية لم تصمد أمام التحقق المستقل، وهي تعتبر مشكوك فيها من قبل المجتمع الفيزيائي الأكبر. وإذا ما لاحظنا مثل هذا التغير بشكل قوي، فسوف يعلمنا ذلك أن شيئًا نلاحظه بأنه ثابت في الكون – مثل شحنة الإلكترون، أو ثابت بلانك، أو سرعة الضوء – قد لا يكون ثابتًا بالفعل عبر المكان أو الزمن.

يُمثّل مخطط فاينمان هذا تشتت إلكترون-إلكترون، والذي يتطلب جمع جميع السجلات الممكنة لتفاعلات الجسيمات. نشأت فكرة أن البوزيترون هو إلكترون يتحرك للخلف في الزمن من التعاون بين فاينمان وويلر، ولكن شدة تفاعل التشتت تعتمد على الطاقة وتُحكم بثابت البنية الدقيقة الذي يصف التفاعلات الكهرومغناطيسية.

لكن نوعًا مختلفًا من التباين قد تم إعادته بالفعل: تتغير ألفا كدالة لشروط الطاقة التي تجري فيها تجاربك.

لنفكر لماذا يجب أن يكون الأمر كذلك من خلال تخيّل طريقة مختلفة للنظر إلى البنية الدقيقة للكون: خذ إلكترونين واحتفظ بهما على مسافة محددة بعيدًا عن بعضهما البعض. يمكن اعتبار ثابت البنية الدقيقة، α، كنسبة بين الطاقة اللازمة للتغلب على التنافر الكهروستاتيكي الذي يدفع هذين الإلكترونين بعيدًا وطاقة فوتون واحد يكون طول موجته 2π مضروبًا في المسافة بين هذين الإلكترونين.

ولكن في كون كمي، توجد دائمًا أزواج جسيم-مضاد جسيم (أو تقلبات كمية) تسكن حتى الفراغ الخالي تمامًا. عند طاقات أعلى، يغيّر هذا قوة التنافر الكهروستاتيكي بين إلكترونين.

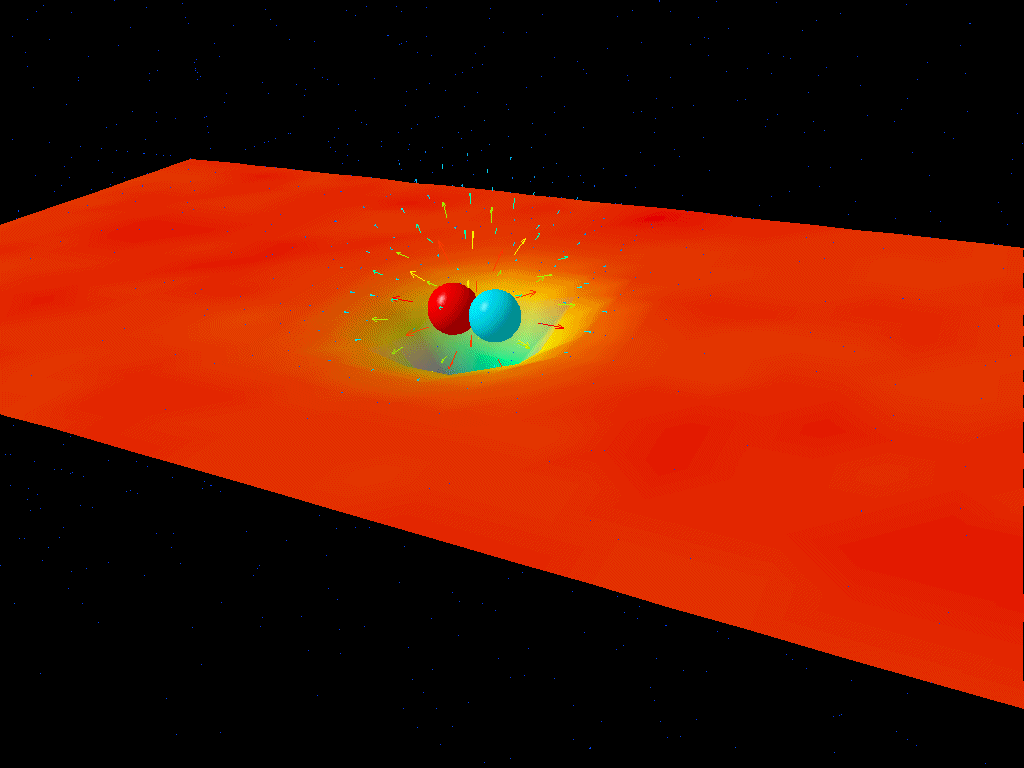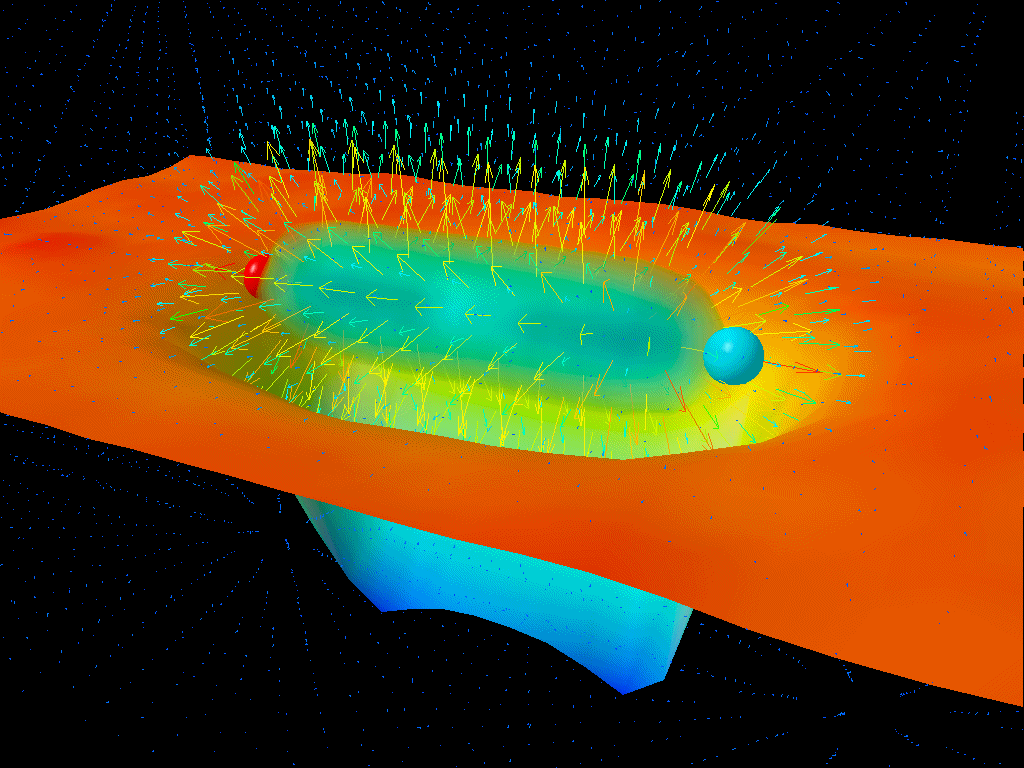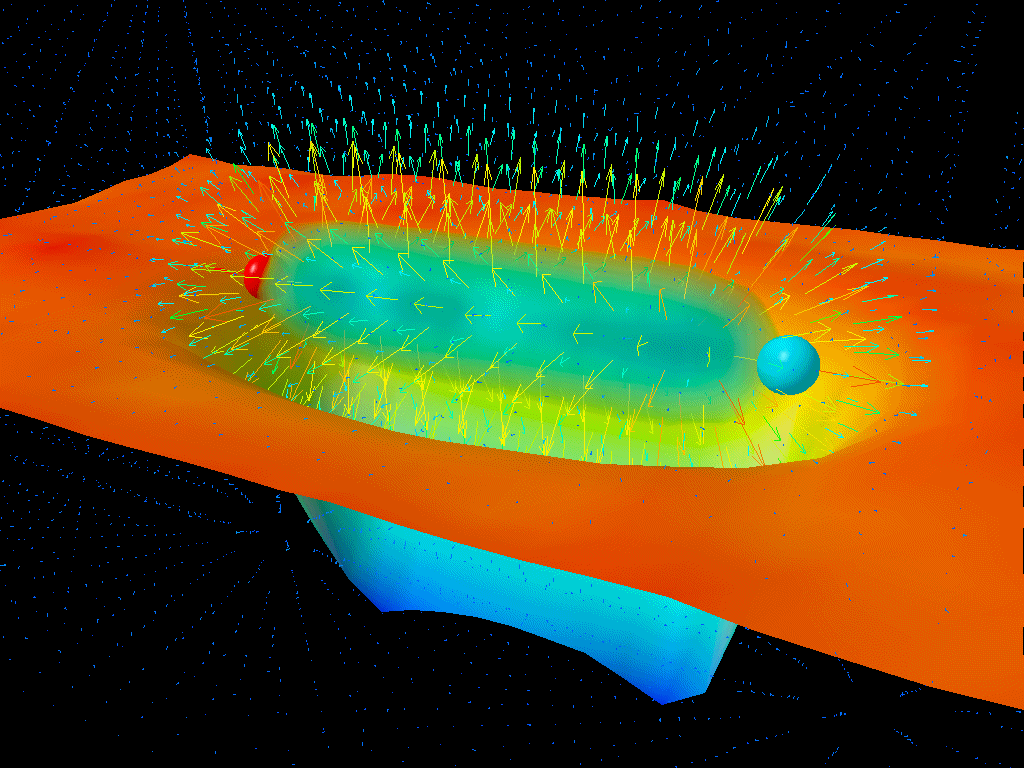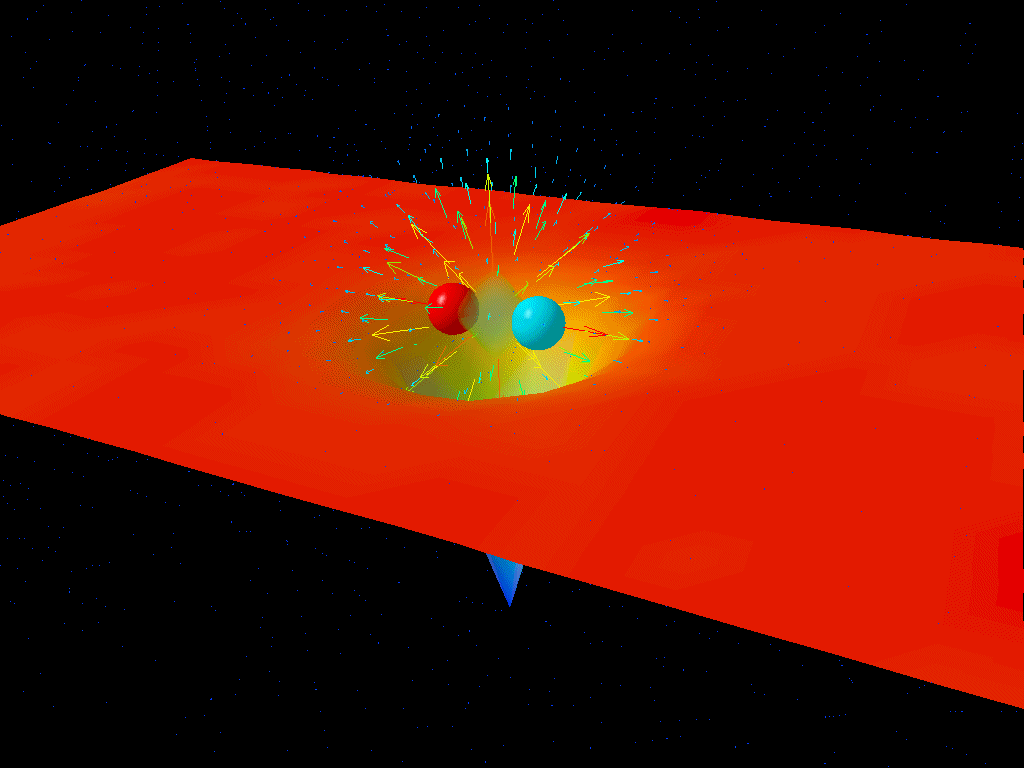
يوضح هذا التصور الديناميكا اللونية الكمية كيف تظهر أزواج الجسيمات/مضادات الجسيمات من الفراغ الكمي لفترات زمنية قصيرة جدًا نتيجة لمبدأ هايزنبرغ للشك. إن الفراغ الكمي مثير للاهتمام لأنه يفرض أن الفضاء الخالي نفسه ليس فارغًا تمامًا، بل مليء بجميع الجسيمات ومضادات الجسيمات والحقول في حالات مختلفة تتطلبها نظرية الحقل الكمي التي تصف كوننا.

والسبب في ذلك بسيط في الواقع: إن أخف الجسيمات المشحونة في النموذج القياسي هي الإلكترونات والبوزيترونات، وفي الطاقات المنخفضة، تكون المساهمات الافتراضية من أزواج الإلكترون-البوزيترون هي التأثيرات الكمية الوحيدة التي تهم من حيث قوة القوة الكهروستاتيكية. ولكن عند الطاقات الأعلى، لا يصبح من الأسهل فقط إنتاج أزواج الإلكترون-البوزيترون، مما يعطيك مساهمة أكبر، بل تبدأ في الحصول على مساهمات إضافية من مجموعات جسيم-مضاد جسيم أثقل.

في الطاقات المنخفضة (العادية) التي لدينا في كوننا اليوم، α تقارب 1/137. ولكن عند مقياس الطاقة الكهروضعيفة، حيث تجد أثقل الجسيمات مثل بوزونات W و Z وبوزون هيغز والكوارك العلوي، تكون α أكبر إلى حد ما: تقارب 1/128. وبشكل فعال، وبفضل هذه المساهمات الكمية، يبدو الأمر كما لو أن شحنة الإلكترون تزداد قوة.

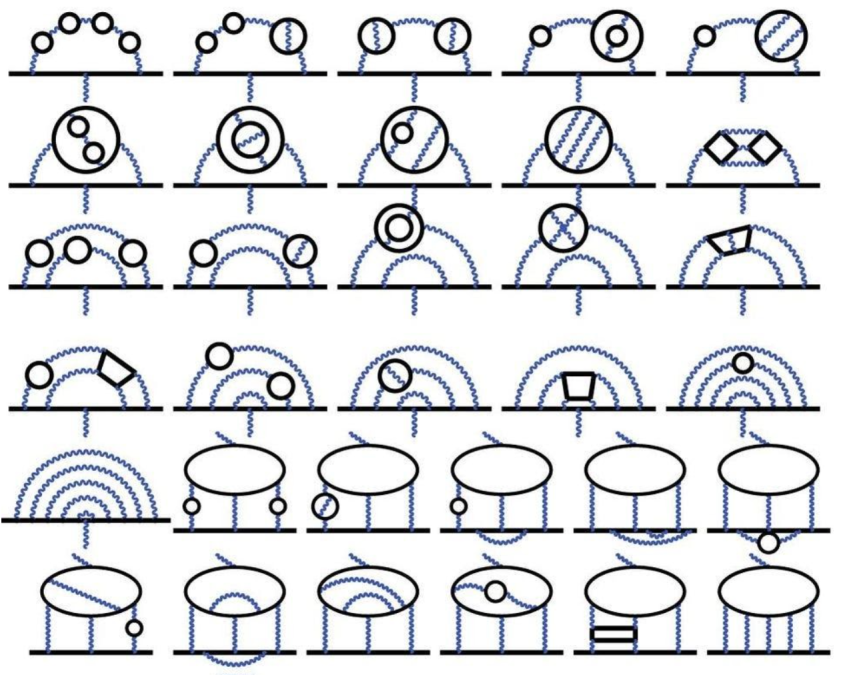
بفضل جهدٍ هائل بذله الفيزيائيون النظريون، تم حساب العزم المغناطيسي للميون حتى رتبة الخمس حلقات. وتبلغ الآن أوجه عدم اليقين النظرية مستوى جزء واحد من ملياري جزء. وهذا إنجازٌ هائل لا يمكن تحقيقه إلا في سياق نظرية المجال الكمومي، وهو يعتمد اعتمادًا كبيرًا على ثابت البنية الدقيقة وتطبيقاته.

يلعب ثابت البنية الدقيقة، α، أيضًا دورًا رئيسيًا في واحدة من أهم التجارب الجارية في الفيزياء الحديثة اليوم، وهي الجهد المبذول لقياس العزم المغناطيسي الجوهري للجسيمات الأولية. بالنسبة لجسيم نقطي مثل الإلكترون أو الميون، لا يوجد سوى عدد قليل من الأشياء التي تحدد عزمها المغناطيسي:

1. الشحنة الكهربائية للجسيم (التي تتناسب طرديًا معها)،
2. عزم دوران الجسيم (التي تتناسب طرديًا معها)،
3. كتلة الجسيم (التي تتناسب عكسيا معها)،
4. وثابت، يُعرف باسم g، وهو تأثير ميكانيكي كمي بحت.

بينما تُعرف الثلاثة الأولى بدقة بالغة، إلا أن g معروفة فقط بدقة أفضل بقليل من جزء واحد من مليار. قد يبدو هذا قياسًا ممتازًا للغاية، لكننا نحاول قياسه بدقة أكبر لسبب وجيه للغاية.

هذا هو شاهد قبر جوليان سيمور شفينغر في مقبرة ماونت أوبورن في كامبريدج، ماساتشوستس. والصيغة هي تصحيح لـ “g/2” كما حسبها لأول مرة عام 1948. وقد اعتبرها أفضل نتيجة له.

في عام 1930، كنا نظن أن قيمة g ستكون 2، بالضبط، كما استنتج ديراك. لكن هذا يتجاهل التبادل الكمي للجسيمات (أو مساهمة مخططات الحلقة)، والتي تبدأ فقط في الظهور في نظرية المجال الكمي. وقد تم اشتقاق التصحيح من الرتبة الأولى بواسطة جوليان شفينغر في عام 1948، والذي ينص على أن g = 2 + α/π. وحتى اليوم، لقد حسبنا جميع المساهمات حتى الرتبة الخامسة، وهذا يعني أننا نعرف جميع حدود (α/π)، بالإضافة إلى حدود (α/π) ²، (α/π) ³، (α/π) ⁴، و (α/π)⁵.

يمكننا قياس g تجريبياً وحسابيًا نظرياً، وما نجد، بشكل غريب جدًا، هو أن التطابق بين الاثنين دقيق جدًا، ولكنه ليس مثالياً. إن الاختلافات بين g من التجربة والنظرية صغيرة جدًا، جدًا: 0.0000000052، مع عدم يقين يبلغ حوالي ±0.0000000010: فرق قدره 5.2 سيغما. ومع ذلك، فإن طريقة نظرية ثانية تُعطي فرقًا أصغر بكثير، مما يشير إلى وجود صعوبة ما في الجانب النظري؛ ستُقرر التجارب بالتأكيد.

إذا كان هناك فرق حقيقي، فقد نكون على شفا فيزياء جديدة تتجاوز النموذج القياسي؛ وإلا، فسنتعلم شيئًا عن افتراضاتنا النظرية بدلاً من ذلك.

مغناطيس كهربائي تجربة ميون g-2 في مختبر فيرميلاب، جاهز لاستقبال حزمة من جسيمات الميون. بدأت هذه التجربة في عام 2017 ولا تزال تجمع البيانات، وقد قللت من عدم اليقين في القيم التجريبية بشكل كبير. نظرياً، يمكننا حساب القيمة المتوقعة بشكل مضطرب، من خلال جمع مخططات فاينمان، والحصول على قيمة تختلف عن النتائج التجريبية. ومع ذلك، يبدو أن الحسابات غير المضطربة، عبر شبكة QCD، تتفق، مما يعمق لغز العزم المغناطيسي الشاذ للميون.

عندما نبذل قصارى جهدنا لقياس الكون – بدقة أكبر، وبطاقات أعلى، وتحت ضغوط استثنائية، ودرجات حرارة أقل، إلخ – غالباً ما نجد تفاصيل دقيقة وغنية ومحيرة. ولكن ليس الشيطان هو الكامن في تلك التفاصيل، بل يكمن فيها أسرار الواقع الأعمق.

إن الجسيمات في كوننا ليست مجرد نقاط تتجاذب وتتنافر وترتبط ببعضها البعض؛ بل تتفاعل من خلال كل الوسائل الدقيقة التي تسمح بها قوانين الطبيعة. وعندما نصل إلى درجات أعلى من الدقة في قياساتنا، نبدأ في الكشف عن هذه التأثيرات الدقيقة، بما في ذلك تعقيدات في بنية المادة يسهل تفويتها عند انخفاض الدقة. يُعد البنية الدقيقة جزءًا حيويًا من ذلك، ولكن معرفة أماكن انهيار أفضل تنبؤاتنا بالبنية الدقيقة قد يكون هو المكان الذي تأتي منه الثورة العظيمة التالية في فيزياء الجسيمات. إن إجراء التجربة الصحيحة هو السبيل الوحيد الذي سنعرف به ذلك.

هذا القسم الأخير من مقال أطول.

إيثان في إجازة هذا الأسبوع. نرجو أن تستمتعوا بـ هذا المقال من أرشيفات Starts With A Bang!