“`html
اشتراك في نشرة البداية مع انفجار
سافر عبر الكون مع الدكتور إيثان سيجل حيث يجيب على أكبر الأسئلة على الإطلاق
“`
نادراً ما تظهر كتابٌ يُغيّرُ وجهة نظر الخبراء في مجالهم حول المبادئ الأساسية، مع إمكانية الوصول والإفادة منه بسهولة لأولئك الذين ليس لديهم خبرةً في هذا المجال. لهذا السبب، مع اقتراب عام 2024 من نهايته، يُعدّ اختيار كتاب مات ستراسلر الجديد الرائع، أمواج في بحرٍ مستحيل: كيف تنشأ الحياة اليومية من المحيط الكوني، اختياراً بديهياً ليكون أفضل كتاب علمي لهذا العام. (نعم، حتى في [[LINK29]]عامٍ كتبت فيهُ أنا نفسي [[LINK29]] كتاباً خاصتي!) ويقود ستراسلر، وهو خبير عالمي مُعترف به في فيزياء الجسيمات (ومُدون علمي مُتواصل)، القارئ في جولةٍ سريعةٍ حول الفيزياء من وجهة نظرٍ مُفاهيمية.
حتى المواضيع الكلاسيكية مثل نسبية غاليليو وجاذبية نيوتن تُقدّم بطرق جديدة، مُيسّرة، مع استبدال المصطلحات التاريخية الشائعة مثل “قانون نيوتن الأول” بمصطلحات أكثر حدسًا مثل “قانون الانجراف”. يأخذنا ستراسلر في رحلات مماثلة عبر مواضيع كلاسيكية أخرى مثل الكتلة والموجات والحقول قبل الدخول في عالم الكم الأقل دراية، والذي يبدو فجأة أكثر سهولة من أي وقت مضى، بفضل الأساس الذي وضعه ستراسلر في أجزاء سابقة من الكتاب. بحلول الوقت الذي نصل فيه إلى قسمي الكتاب الأخيرين، بما في ذلك قسم عن بوزون هيغز، يبدو الأمر شبه مُتوقع. على الرغم من غرابة وغموض بوزون هيغز لدى الكثيرين، إلا أنه يبدو، بفضل ستراسلر، وكأن الكون لن يكون منطقيًا بدونه.

“`html
البروتون ليس مجرد ثلاثة كواركات وغلوونات، بل بحر من الجسيمات والمضادات الكثيفة بداخله. كلما نظرنا بدقة أكبر إلى البروتون وكلما زادت الطاقة التي نستخدمها في تجارب التشتت غير المرنة العميقة، كلما وجدنا المزيد من البنية الفرعية داخل البروتون نفسه. يبدو أنه لا يوجد حد لكثافة الجسيمات بداخله، ولكن ما إذا كان البروتون مستقرًا بشكل أساسي أم لا، فهو سؤال لم يُجَب عنه بعد.
“`
نادراً ما يحدث لي – أناُ بنفسي فيزيائي نظري حاصل على درجة الدكتوراه – أن أقرأ كتابًا في الفيزياء وأجد نفسي أتوقف لأقدر وأهضم شيئًا تعلمته (وُدرّسته) عشرات المرات من قبل، لأنني أُفصّله في طريقة جديدة، غير مألوفة، ومع ذلك عميقة. لكن كتاب ستراسّلر استغرق مني شهورًا للانتهاء منه بالطريقة الأمثل: لأنه على الرغم من بساطة أسلوب الكتابة، إلا أنّه كان يحتوي على حقائق كثيفة المعلومات كنت أجدها ممتعة للغاية للتوقف والتأمل فيها طويلاً، حيث ساعدتني في تحسين وتطوير فهمي للعديد من جوانب الفيزياء بنفسي، وكذلك كيفية شرحها للآخرين، بما في ذلك (مؤخرًا جدًا) هنا و هنا.
بسبب مدى الاستثنائيّة لهذا الكتاب، تواصلتُ مع ماثيو وسألتهُ إن كان مستعدًا لإجراء مقابلة معي، غالبًا حول كتابه ولكن تتضمن بعض الأسئلة تتجاوز ما قد يجده القارئ العادي داخله. وافق بكرم، ولذا يسعدني أن أقدم لكم حوارًا أسئلة وأجوبة مع الأستاذ ماثيو ستراسلر، مؤلف كتاب أَموَاجٌ في بحرٍ مستحيل، والذي يُعدّ اختيار Starts With A Bang لأفضل كتاب علمي لعام 2024!
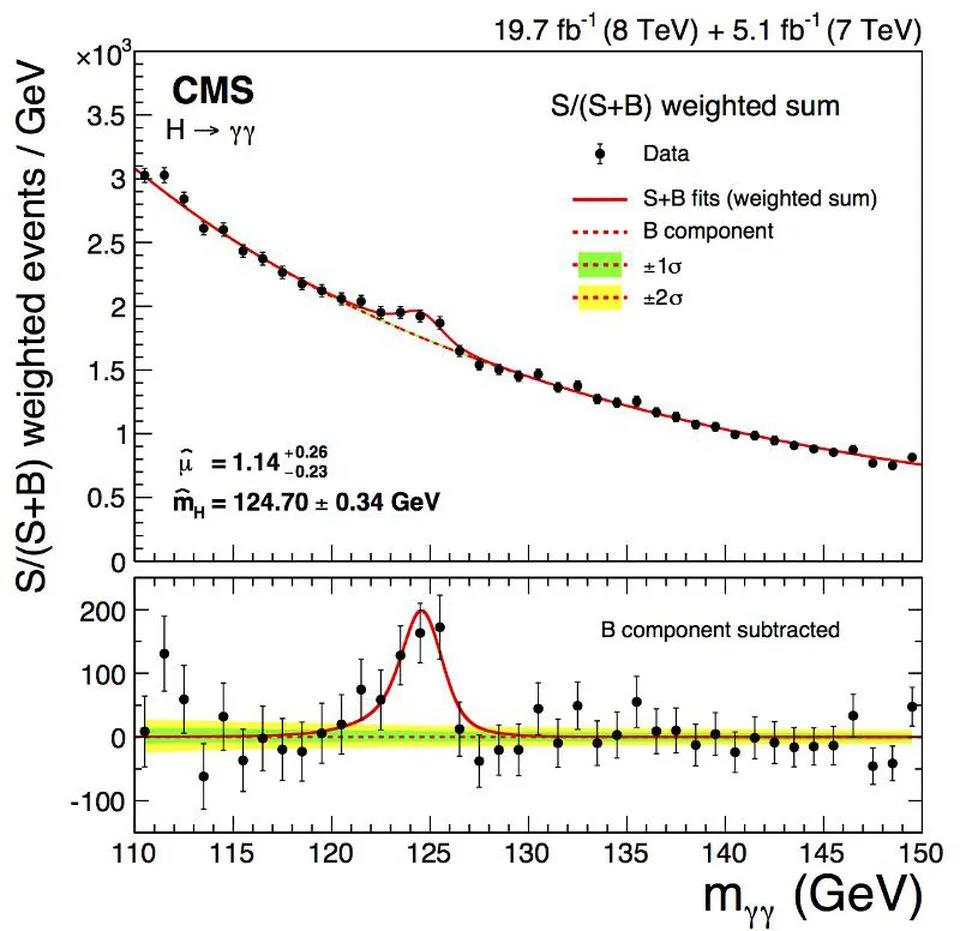
أُعلن عن أول اكتشاف قوي، ذي مستوى 5-سيغما، للجسيم البوزون الهيجز قبل بضع سنوات من قبل كل من التعاونين CMS و ATLAS. لكن جسيم البوزون الهيجز لا يُظهر ذروةً واحدةً واضحةً في البيانات، بل بروزًا مُتشتّتًا، بسبب عدم اليقين المتأصل في كتلته. كتلته البالغة 125 جيڤي/سي² تشكّل لغزًا للفيزياء النظرية، لكنّ المُختصين التجريبيين لا داعي للقلق: فهو موجود، يمكننا خلقه، والآن يمكننا قياس خصائصه ودراستها أيضًا. كان الاكتشاف المباشر ضروريًا للغاية لكي نتمكّن من القول بشكل قاطع بأنه موجود.
إيثان سيجل (ES): لقد مضى الآن أكثر من 12 عامًا على إعلان اكتشاف بوزون هيغز: آخر جسيم أساسي يُكتشف في النموذج القياسي. ورغم أن معظم الناس سمعوا الآن عن بوزون هيغز، إلا أن قلة قليلة يفهمون ماهيته أو ما يقوم به. كيف حفز هذا الجسيم، والسوء فهم حوله، كتابة كتابك الجديد، “أمواج في بحر مستحيل”؟
مات ستراسلر (MS): إنني أشعر دائمًا بالقلق عندما يقلل الفيزيائيون من أهمية علومنا كثيرًا، بحيث يكون النتيجة مضللة أو حتى خاطئة. وأشعر أن هذا يُقلل من ذكاء قرائنا ومستمعينا. وللسوء، غالبًا ما تتناقض تفسيراتنا السيئة مع تفسيراتنا الجيدة، مما يخلق تناقضات منطقية يجعل من المستحيل على غير الخبير فهم ما نقوله. يجب أن يكون هناك طريقة أكثر ذكاءً وأمانة لنقل دروس العلم.
تُقدمُ وصفاتُ بوزون هيغز والحقلِ المُرتبطِ به مثالاً مُثاليًا. فالحقلُ الهيجزِيُّ جزءٌ مُهمٌّ من الكون؛ لأُدرجهُ في قائمةِ العشرِ الأوائلِ من المكوناتِ الأساسيةِ للحياة. وهو شيءٌ ينبغي علينا شرحُهِ جيدًا. ومع ذلك، في كلِّ مقالٍ وكتابٍ رأيتُهُ في هذا الموضوع، فإنّ وصفَ الحقلِ الهيجزِيّ مُعيبٌ. لذا اعتبرتهُ تحديًا شخصيًا لكتابةِ كتابٍ يحتوي على شرحٍ صحيحٍ، غيرِ تقنيّ، للحقلِ الهيجزِيّ وكيفية عملهِ.
ومع ذلك، في النهاية، كان الحقلُ الهيجزِيُّ في الواقعِ جزءًا ثانويًا. فجوهرُ الكتابِ هو قصتهُ عن الحقولِ وكيفية نشوءِ الجسيماتِ الأوليةِ منها، ولماذا جسيمٌ أوليٌّ مثل الإلكترونِ أكثرُ من موجةٍ تهتزُّ بسرعةٍ من نقطةٍ صغيرةٍ. بمجرد وضوحِ هذا، يصبحُ فهمُ ما يفعلهُ الحقلُ الهيجزِيّ ولماذا هو مهمٌّ جدًا، وما معنى اكتشافُ بوزون هيغز، أسهلَ بكثير.

عندما تُستعاد التناظر (الكرة الصفراء في الأعلى)، يكون كل شيء متناظرًا، ولا يوجد حالة مفضلة. عندما ينكسر التناظر عند طاقات منخفضة (الكرة الزرقاء، أسفل)، فإن نفس الحرية، من جميع الاتجاهات المتساوية، لم تعد موجودة. في حالة تناظر الكهروضعفي (أو هيغز)، عندما ينكسر، تحدث عملية تلقائية، مما يعطي كتلة للجسيمات في الكون.
ES: يجب عليّ أن أعترف بأنه، عندما اكتشفت البشرية حقلاً هيغز لأول مرة، ابتكرت ما أدركت الآن أنه “خطأ فيزيائي” كما تسمونه، حيث أشبهت فيه مجال هيغز بظاهرة المطر، والجسيمات التي تكتسب كتلة بمثابة إسفنج جافة تمتص هذا المطر. هناك العديد من “الأخطاء” الأخرى من هذا القبيل فيما يتعلق بِمجال هيغز وبُوزون هيغز معاً. ما هو الخطر الذي تراه في “الأخطاء” مثل هذه؟ هل تُضر هذه “الأخطاء” بالتصور العام للعلوم؟
MS: أحبّ “خطأك” أكثر من معظمها، لأنه يتجنب تشويه مفهوم الكتلة. تلك التي تشبه مجال هيغز بِحساء أو مِهلٍ يُملأ الفراغ، وتقول إن مجال هيغز يُمنح الكتلة للأشياء عن طريق إبطائها، هي حرفيًا من العصور الوسطى! إنها تنتهك قانونين من قوانين نيوتن للحركة، مُشجعةً على تخيّل، بشكل خاطئ، أن امتلاك الكتلة يُصعّب حركة الجسم.
كل هذه الجسيمات (حتى الخاصة بك) تميل إلى الإيحاء بأنّ مجال هيغز يُضفي على الجسيمات حجمًا أكبر أو بطءًا. ومع ذلك، فإنّ ما يحدث بالفعل يتعلق بالطاقة التي تحملها الجسيمات بداخلها. علاوة على ذلك، على الرغم من أنّنا العلماء (بما في ذلك أنا) نقول جميعًا، كاختصار، إنّ “مجال هيغز يُمنح الجسيمات كتلها”، إلا أنّ ذلك ليس صحيحًا تمامًا؛ فمجال هيغز لا يُمنح جسيمًا طاقةً، أو أي شيء آخر. إنه فقط يُغيّر مقدار الطاقة المطلوبة لوجود الجسيم. لكي نرى لماذا ذلك صحيح، يجب أولًا فهم أنّ الجسيمات الأولية كائنات تهتز.
بشكل عام، لست متعصبًا بشأن الفيبس؛ فبعضها غير ضار في الغالب. بالإضافة إلى ذلك، عندما يكون الوقت قصيرًا، قد يكون الفيبس هو الخيار الوحيد المتاح. ومع ذلك، أشعر بأن المتحدث أو الكاتب يجب أن يوضح دائمًا عندما يكون البيان فيبس، حتى يعرف المستمعون بعدم أخذه على محمل الجد، ويعرفون الحاجة إلى البحث بشكل أعمق إذا أرادوا الحقيقة حقًا. وأعتقد أن الفيبس يمكن تجنبها في الغالب في المقالات والكتب والمقاطع المرئية الطويلة.
المخاطر الكامنة في “الفيب” تتمثل في عدم وجود “فيب” منعزل. عندما تُعرض على الشخص مجموعة من “الفيبات” والحقائق المتناقضة مع بعضها البعض، كيف يمكن لأيّ شخص أن يعرف أيّها يُصدّق؟ إنها حالة مُربكة بطبيعتها، وللأسف، يلوم بعض الناس أنفسهم، مُعتقدين أنهم ليسوا أذكياء بما يكفي لفهم ما يجري. ويستنتج آخرون العكس: أن العلماء لا يُدركون ما يتحدثون عنه! ويُنظر آخرون إلى العلماء على أنهم غير قادرين جماعياً على شرح الأمور – وهنا، أخاف أن يكونوا على صواب إلى حد ما. لا تُعدّ أيٌّ من هذه الاستنتاجات جيدة للعلم وعلاقته بالمجتمع. بعد كل شيء، يتم تمويل أبحاث العلوم من قبل الصناعة ومن خلال الضرائب، وبالتالي من قبل غير العلماء، الذين يستحقون تفسيرات واضحة وصحيحة وموثوقة للعلم الذي دعموه.
لقد قضيت وقتًا طويلًا في تطوير مجموعة متماسكة من التفسيرات الدقيقة المتسقة منطقيًا مع بعضها البعض. (عندما تفكر في الأمر، فإنّ صياغة قصة متسقة من تفسيرات صحيحة أسهل بكثير من فعل ذلك من تفسيرات خاطئة!) آمل أن تُقنع كتابي بعض زملائي باعتمادها.


تُظهر هذه الصورة سفينة حرس السواحل الأمريكية قاطرة مونرو وهي تغادر الميناء في سان دييغو، كاليفورنيا. طالما أن هذه السفينة لا تتسارع، فإنّ المُلاحظ الذي يوجد أسفل سطح السفينة وليس لديه نافذة إلى الخارج لا يستطيع معرفة ما إذا كانت سفينته ساكنة أو في حركة مستمرة بالنسبة للعالم الخارجي.
ES: كتابك يقدم خمسة أقسام رئيسية خلفية – الحركة، والكتلة، والموجات، والحقول، والكمّ – قبل الوصول أخيراً إلى الأقسام المُختتِمة حول هيغز والكون. في كلٍّ من تلك الأقسام الأساسية، تأخذ شيئاً من المبادئ المعروفة (مثلًا، مبدأ النسبية) وتُعيد صياغته بطريقة غير تقليدية (مثلًا، “قانون الانجراف”). ما هي عملية تفكيرك وراء ربط هذه المفاهيم المألوفة لدى الفيزيائيين بطريقة نادراً ما يتصورها الفيزيائيون؟
MS: بصفتي معلمة ومدونة، أدرك تمامًا كيف يمكن أن تُعيق الكلمات التي يستخدمها العلماء شرحنا. في بعض الأحيان، يبدو مصطلح علمي جديرًا بالاحتفاظ به، لكن في كثير من الأحيان يكون مضللًا أو غامضًا أو مجرد تجريد غير ضروري. ومع ذلك، فإن كل حالة تتضمن تفكيرها الخاص. سأقدم لكم بعض الأمثلة.
على سبيل المثال، يستخدم العلماء مصطلح “الطاقة الحركية” للإشارة لطاقة الحركة. لكن ما الخطأ، في كتاب، باستخدام مصطلح “طاقة الحركة” ببساطة؟ إن القيام بذلك يُزيل كلمة تجريدية غير ضرورية، مما يقلل من عدد الأشياء التي يحتاج القارئ المبتدئ إلى تتبعها.
لقد أشارتُ إلى “قانون نيوتن الأول” باسم “قانون الانجراف” لأن من غير المهم على الإطلاق أنه قانونه الأول وليس سابعه. بدا من الأفضل أن يتذكر القراء القانون ليس باسمه، بل بمعناه: أن الجسم المعزول الذي يسير بحركة منتظمة سيتحرك بنفس السرعة والاتجاه إلى الأبد.
كان الاختيار الثالث، والأهم، هو استبدال كلمة “جسيم” في الثلث الأخير من الكتاب بكلمة “موجة-جسيم”، وهي مصطلح من عشرينيات القرن الماضي، تستخدمه حاليًا بعض العلماء الآخرين، بمن فيهم نيل ديجراس تايسون وفرانك ويلزيك. تكمن المشكلة في تسمية الإلكترون بـ “جسيم”، لأنه يُثير على الفور تخيل جسم على شكل نقطة صغيرة. ولكن في الواقع، في نظرية المجال الكمومي (اللغة الحديثة لفيزياء الجسيمات)، لا يكون الإلكترون قط نقطة. بل يتوزع دائمًا إلى درجة أكبر أو أصغر، وهو موجهي الشكل بطرق مختلفة، بما في ذلك حقيقة جوهرية أنه يهتز باستمرار. ما يجعله “شبيهاً بالجسيم” ليس شكله، بل عدم قابلية انقسامه – حقيقة أنه يسافر وحدةً لا تتجزأ.
يُجسّد إضافة اللاحقة “-icle” إلى كلمة “موجة” كلاً من شكل الإلكترونات وحقيقة أنها تأتي بوحدات فردية – بحيث لا يمكن تقسيم الإلكترون إلى أجزاء. بمعنى آخر، إنّ كلمة “جسيم” تُنشئ مفاهيم خاطئة حول ماهية الإلكترونات وأقاربها، بينما كلمة “موجة-جسيم” تُفتح عقولنا على الأفكار غير المألوفة اللازمة لفهم الإلكترونات بشكل أفضل.
بالتأكيد، كل خياراتي من هذا النوع هي أحكام شخصية، وأتصور أن بعض زملائي والقراء الأكثر تقدمًا قد لا يوافقون على بعضها. لكنني آمل أن يجد معظم القراء فائدتها، على الأقل في سياق كتابي.
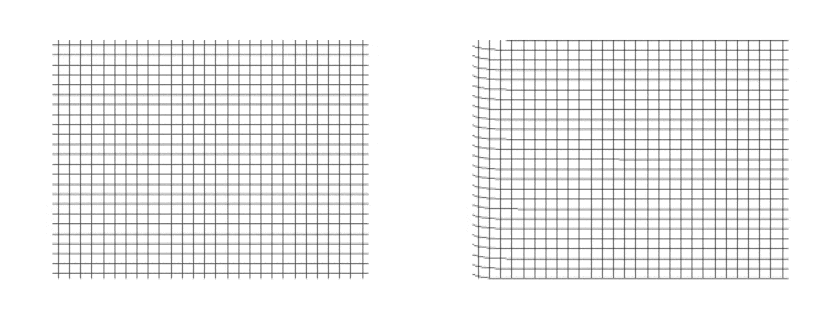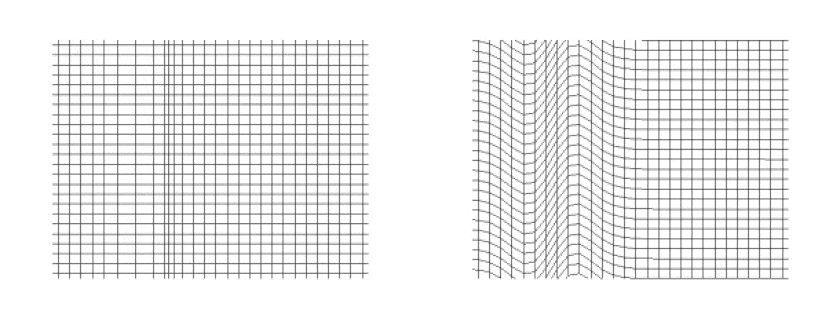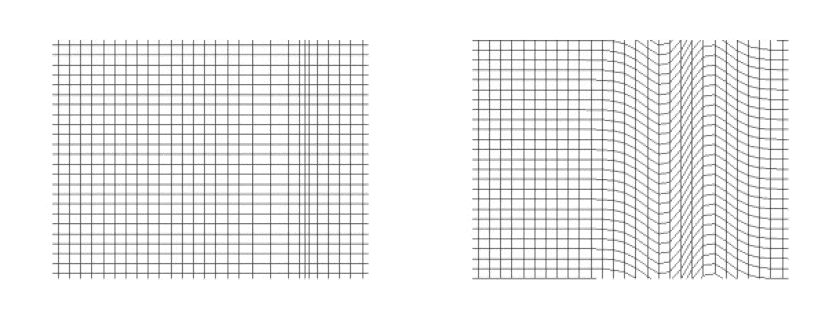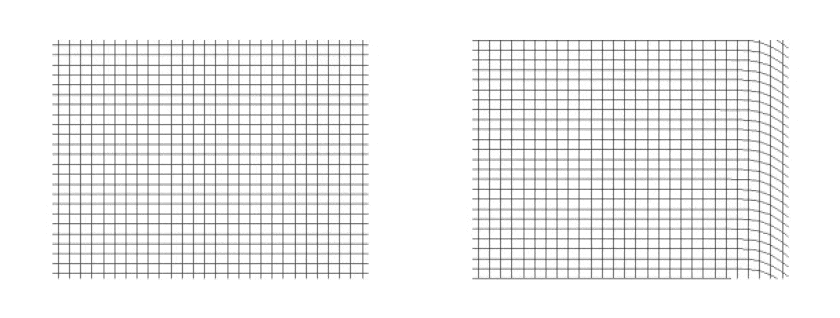

تُوضّح هذه الصورة المُقارنة نوعين من الموجات المُنتقلة: موجة ضغط مُستوية، أو موجة طولية P في اليسار، إلى جانب موجة عرضية S في اليمين. بينما يمكن لموجات P الانتقال عبر المواد الصلبة والسوائل والغازات، فإن موجات S لا تستطيع إلا الانتقال عبر المواد الصلبة.
ES: نظرًا لأهمية مفهوم الموجات ليس فقط في الكتاب، بل وفي الفيزياء الكمومية بشكل عام، فقد خصصت وقتًا كبيرًا لمناقشة ثلاثة مفاهيم: الوسط، والحقل، والموجة. ففي الموجات المألوفة مثل الموجات الصوتية، أو الموجات الزلزالية، أو الموجات المائية، من السهل تحديد كلّ من هذه المفاهيم الثلاثة. ولكن في أنواع معينة من الموجات، نجد فقط الحقل والموجة، مما يجعلنا نتساءل عما إذا كان هناك وسط على الإطلاق. ماذا ستقول لشخصٍ لا يستطيع فهم مفهوم الحقل (أو الموجة) من دون وسط؟
MS: للتأكد من وضوح نقطة انطلاقنا، دعونا نأخذ مثالا. هواء الغلاف الجوي مادة ممتدة… وسط. ضغط الهواء، وهو خاصية للهواء قد تتغير عبر الزمن والمكان، هو مجال، موجود في جميع أنحاء الغلاف الجوي. وأخيرًا، يمكن اعتبار الموجات الصوتية بعدة طرق. عادةً ما نراها موجات في الهواء (موجات الوسط). ولكن يمكننا أيضًا اعتبارها موجات في ضغط الهواء (موجات مجال الوسط).
جميع الموجات المألوفة التي ذكرتها تتضمن اضطرابًا في مادة… وسط. وكل المجالات المألوفة، مثل ضغط الماء أو كثافة الهواء، هي خصائص للوسط. ومع ذلك، فإن الموجات الضوئية (بما في ذلك الضوء المرئي، وموجات الراديو، والميكروويف، إلخ) تُثير الحيرة. إنها بالتأكيد موجات في المجالات – المجالات الكهربائية والمغناطيسية. ولكن هل هذه المجالات خصائص للوسط؟
افتَرضَ فيزيائيّو القرن التاسع عشر أنهم يجب أن يكونوا كذلك. ودعوا ذلك الوسط “الأثير المُضيء”، وحاولوا إيجاد أدلّة عليه، ففشلوا. ثمّ في عام 1905، ادّعى أينشتاين عدم وجود مثل هذا الوسط، وأن الحقول الكهربائية والمغناطيسية موجودة ببساطة من تلقاء نفسها. فكرة مجنونة، كأن ضغط الهواء يمكن أن يُفهم في غياب الهواء. أُشبهها في الكتاب بابتسامة القطّ الشبيه بالثعلب – ابتسامة بلا قطّ.
بالمناسبة، غيّر أينشتاين رأيه في هذا الأمر بعد اختراع نظريته في الجاذبية عام 1915، ما دفعه إلى اعتبار الكون وسيطًا، والجاذبية ناجمة عن انحناء هذا الوسط، و(بحلول عشرينيات القرن العشرين) الأثير المُضيء جزءًا من هذا الوسط نفسه. غالباً ما يتبع مُنظّرو الأوتار هذا المنطق، مُعتَبرين بُعداً إضافياً للفضاء وسيطاً غريباً قد تتضمّن خصائصه الحقول الكهربائية والمغناطيسية، بالإضافة إلى حقول أخرى. هذا موضوعٌ لسردٍ آخر (انظر السؤال 9).
ومع ذلك، حتى لو كان هذا صحيحًا، هناك شيء غريبٌ حقًا يحدث. فالنسبية لأينشتاين تُفيد بأنَّ إذا كانت موجات الضوء أو موجات الجاذبية أو الموجات الكونية الأخرى لها وسط، فإنَّ هذا الوسط يجب أن يتمتع بخصائص لا يمكن لأي مادة عادية أن تمتلكها. هذا موضوعٌ كبير في الكتاب.
ومع ذلك، عندما نعود لسؤالك، ماذا لو كان أينشتاين محقًا في عام 1905، وأنَّ الحقول الكهربائية والمغناطيسية ليس لها وسط – كيف يجب علينا التفكير في هذا الابتسامة بدون قطة؟ من الصعب القول. ربما يكون هذا من تلك الحالات التي تُؤدي فيها جهل الفيزيائيين، أو قيود الدماغ البشري، إلى طرح سؤال لا يوجد له إجابة. لذا، لمن يُعاني من مفهوم الحقل أو الموجة بدون وسط، سأقول: أنت لست وحدك. فالعلماء يُعانون أيضًا.
إن الأمر كله مُهينٌ إلى حدٍّ كبير: فبالرغم من معرفتنا الكبيرة بمجالات الطبيعة، إلا أننا لا نعرفُ شيئًا تقريبًا عن أصلها ومعناها. أعتقد أن الوقت لم يحن بعدُ لتخمين كيف ستنتهي قصة الأمواج والمجالات والإعلام في النهاية.
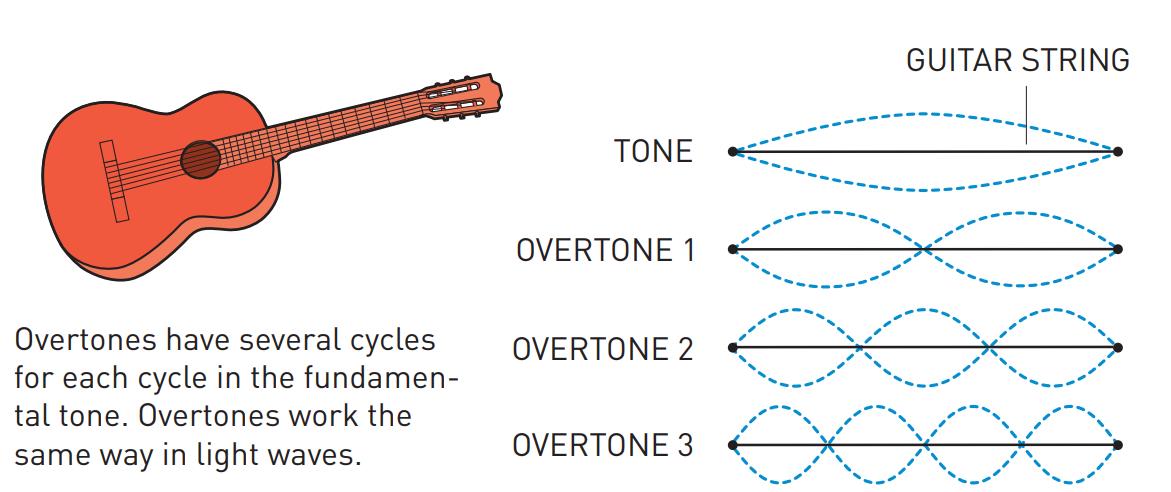

بينما تُصدر وترٌ على غيتارٍ ترددًا أساسيًا يهتزّ عنده، مُنتجًا توضيحَ “النغمة” في اليمين، يمكنك أيضًا “ربط” عقدٍ على الوترِ لإجباره على الاهتزاز بتردداتٍ أعلى: التوافقيات. تُوضّح أول ثلاث توافقيات ربط عقدٍ على الوترِ عند نصف، وثُلث، وربع طول الوتر الأصلي، على التوالي.
ES: كتبتُ هايكو رائعًا في كتابك الذي أطلقت عليه اسم “هايكو أينشتاين”. يقول، بكل بساطة:
E يساوي f h،
و E يساوي m c تربيع؛
من هذه البذور، العالم.
إذا تذكرنا أن h و c هما ثابتان فقط، فإننا نجد أن m، كتلة الجسيم، تتناسب مع f، أو التردد. هذا سيبدو غريبًا جدًا لشخص لم يقرأ كتابك. من الناحية المفاهيمية، كيف يمكن أن ترتبط الكتلة، التي نفكر فيها عادةً على أنها خاصية جوهرية لجسيم كمي، بخصائص موجية مثل التردد؟
MS: بالتأكيد، يبدو العلاقة غريبة، لكن دعني أرَى إذا استطعتُ رسمها بسرعة. الجزء الأكثر شيوعًا هو هذا: بالنسبة لأي جسم يسافر كوحدة، بما في ذلك الجسيم الأولي، تُظهر كتلته، كما نتعلم من صيغة أينشتاين E=mc²، كمية الطاقة المخزنة بداخله.
من المهم هنا أن كلمة “جسيم” مُضللة، كما ذكرت [في سؤاليْن سابقَين]. بدلاً من نقطة صغيرة، فإن الإلكترون أو أي جسيم أوليّ هو كيانٌ مهتزٌّ صغيرٌ – موجةٌ لا تُجزّأ، تُسمى أحيانًا “موجة-جسيم”. ببساطة لأنّه يهتزّ، فإنه يمتلك طاقةً. وهذه الطاقة، بفضل السطر الثاني من الهيكو، هي مصدر كتلته.
لكن الفيزياء الكمومية تُخبرنا بشيءٍ أكثر إعجابًا وغرابةً من ذلك: أن الطاقة 𝐸 المخزنة داخل جسيم الموجة-الجسيم تتناسب تناسبًا طرديًا مع التردد 𝑓 الذي يهتزّ به. الصيغة التي تُبيّن هذا الأمر هي 𝐸 = 𝑓 ℎ، السطر الأول من الهيكو.
وبالتالي، كتلة جسيم الموجة-الجسيم الأوليّ، الكيان المهتزّ، تتناسب تناسبًا طرديًا مع الطاقة التي يحملها داخله، والتي بدورها تتناسب تناسبًا طرديًا مع تردد اهتزازه.
أدركُ أن هذه اللمحة المُوجزة للغاية عن أول مئتي صفحة من الكتاب صعبة المتابعة. بل إنّ من أهم الأسباب التي دفعتني لكتابة هذا الكتاب هو عرض هذه القصة بعناية ووضوح. كان دورُ الهايكُو هو تلخيص تلك القصة في شكلٍ مُتذكرٍ. أُسعدُ بأنك أعجبك!

تُظهر هذه إعادة بناء مسارات الجسيمات حدثًا مرشحًا لحِجْز الهيغز في مُكتشف أتلانتس المُوجود في مُصادم الهدرونات الكبير في سيرن. لاحظ كيف أنّه حتى مع وجود توقيعات واضحة ومسارات عرضية، يوجد زخات من الجسيمات الأخرى؛ وهذا بسبب حقيقة أن البروتونات جسيمات مركبة، وبسبب حدوث عشرات من التصادمات البروتونية-البروتونية مع كل عبور حزمة. عند طاقات أعلى، تصبح الاكتشافات التي لا تظهر عند الطاقات الأدنى ممكنة. إن مُكتشفات الجسيمات الحديثة تشبه طبقات الكعكة، بقدرتها على تتبع حطام الجسيمات من أجل إعادة بناء ما حدث بالقرب من نقطة التصادم قدر الإمكان.
“`
ES: بعض الكميات التي نعرفها، مثل الكوارك الأعلى والبوزون هيغز، تعيش لفترة قصيرة للغاية. على الرغم من أنك لا تُعنى بذلك عند طرح مفهوم عدم اليقين الكمي، إلا أن هناك أيضًا علاقة مهمة بين الطاقة والوقت. إذا قمت بإنشاء 1000 إلكترون وقياس كتلها، فسأحصل على نفس الإجابة في كل مرة. ماذا يُخبرنا ذلك، وهل هناك أي دروس متعلقة بالموجات، إذا قمنا بإنشاء 1000 كوارك أعلى أو 1000 بوزون هيغز، لن نقيسها جميعًا بنفس الكتلة؟
MS: كما هو الحال مع العديد من المفاهيم في فيزياء الجسيمات، فإننا على دراية بالفعل بتأثير مماثل للغاية في سياق الآلات الموسيقية.
إذا ضربت جرسًا، فستسمع نغمة واضحة، رنانة — بِينغ! — بتردد محدد، ونغمة موسيقية محددة. في كل مرة تضربه، ستكون اهتزازاته بنفس التردد، مما يعطي نفس النغمة. والحقيقة نفسها تنطبق على الكون؛ إذا ضربته بالطريقة الصحيحة تمامًا وأنتجت إلكترونات ثابتة، فسوف يهتز كل إلكترون دائمًا بنفس التردد، وبالتالي سيكون له نفس الكتلة مثل كل الإلكترونات الأخرى.
ولكن إذا كنت ستغطي جرسًا، ربما بوضع يدك عليه برفق أو تغطيته ببطانية، فإن تأثير ضربه سيكون مختلفًا. ستسمع صوتًا أكثر تشابهًا بـ “كِلَك”; ستكون نغمة موسيقاه أقل وضوحًا، وسيتلاشى صوت الجرس بسرعة كبيرة. وهذا ليس صدفة، لأن هاتين الحقيقتين مرتبطتان ارتباطًا وثيقًا. لأي جسم مهتز، إذا قمت بتخميد الاهتزاز كما فعلت للجرس، فإن الاهتزاز سيتلاشى بسرعة وسيتدنى تردده الاهتزازي.
تُفسّر نفس الفكرة (والرياضيات نفسها!) تمامًا كيف تعمل الأشياء بالنسبة للكواركات العُليا أو الجسيمات الأخرى قصيرة العمر. إنّ الكوارك العلوي قصير العمر لأنّ اهتزازه مُخمّد بقوة النووي الضعيفة وقوة هيغز، والتي تسبّب، معًا والفيزياء الكمية، تحلّله، مُحوّلةً إياه إلى بوزون دبليو وكوارك أسفل. يُسبب التخميد أيضًا أن يكون لتردد الكوارك العلوي تعريفًا غير دقيق، وبالتالي فإنّ قياسًا دقيقًا لكتلته لن يُعطي نفس الإجابة تمامًا في كل مرة.
ومع ذلك، فإنّ المتوسط على العديد من القياسات ثابت. هذا المتوسط هو ما يُعرّفه العلماء بـ “كتلة الكوارك العلوي”.

يُفسّر النموذج القياسي لفيزياء الجسيمات ثلاثة من القوى التقليدية الأربع (باستثناء الجاذبية)، ومجموعة الجسيمات المكتشفة الكاملة، وجميع تفاعلاتها. يوجد قوة خامسة، وهي قوة هيغز، موجودة أيضًا ضمن سياق النموذج القياسي. يُثير جدلًا ما إذا كانت هناك جسيمات وتفاعلات إضافية يمكن اكتشافها باستخدام المصادمات التي يمكن بناؤها على الأرض، لكن العديد من الألغاز لا تزال دون إجابة.
الائتمان: مشروع تعليم الفيزياء المعاصرة/CPEP، DOE/NSF/LBNL
ES: في الفيزياء، غالبًا ما نتحدث عن القوى الأساسية الأربع: القوة الكهرومغناطيسية، وقوة الجاذبية، والقوة النووية القوية، والقوة النووية الضعيفة. غالبًا ما يذكر الفيزيائيون أنه في بعض المراحل المبكرة جدًا من تاريخ الكون، تم توحيد القوة الكهرومغناطيسية والقوة الضعيفة في قوة واحدة: القوة الكهروضعيفة. ومع ذلك، في كتابك، تتحدث عن خمس قوى أساسية، وتذكر قوة هيغز كالخامسة. هل أهمل الفيزيائيون هذه القوة لعدة أجيال؟ لماذا تقول إن هيغز هي قوة أساسية مستقلة بذاتها، بينما لا تكون القوى الأخرى كذلك؟
MS: حسنًا، كمقدمة، يجب أن نكون حذرين قليلاً بشأن القوة الكهرومغناطيسية والقوة الضعيفة؛ فإنهما ليسا في الواقع موحدتين في قوة واحدة. بدلاً من ذلك، ما يحدث بالفعل هو إعادة تنظيمها إلى قوتين كهروضعيفتين: قوة الأيزوسبين الضعيفة وقوة الشحنة الفائقة.
عن قوة هيغز؛ كلا، لم تُهمَل. على سبيل المثال، عندما كنتُ طالبًا دراسات عليا في مركز تسريع جسيمات ستانفورد الخطي (SLAC) في أوائل التسعينيات، ألقى بي. جي. بيوركِن، فيزيائيٌّ عظيمٌ توفّي مؤخرًا، محاضرةً كاملةً لمجتمع SLAC حول قوة هيغز. (أسس بيوركِن، إلى جانب فاينمان، الإطار النظري الذي أدّى إلى الاكتشاف التجريبي للكواركات).
لكن هناك بعض الأسباب التي أدت إلى التقليل من أهمية قوة هيغز. أولًا، لم يكن واضحًا حتى عشرينيات القرن الحادي والعشرين، عندما تم اكتشاف و دراسة بوزون هيغز في مصادم الهادرونات الكبير، أن حقلاً هيغز موجود بالفعل وأنّه ربما يكون حقلاً أوليًا. وقبل ذلك، لم نكن واثقين تمامًا من أن قوة هيغز أساسية مثل الكهرومغناطيسية. ثانيًا، على الرغم من أن قوة هيغز تتبع منطقيًا من وجود مجال هيغز، وبعض آثارها مُلاحظة (انظر السؤال السابق)، إلا أنها لم تُقاس بشكل مباشر كسحب بسيط بين جسيمين. وسوف يستغرق الأمر بعض الوقت قبل إمكانية هذا القياس. ثالثًا، بينما تستند القوى الأربعة الشهيرة التي ذكرته على رياضيات أنيقة تضمن امتلاكها العديد من الخصائص الخاصة، فإن قوة هيغز بسيطة بالمقارنة. ولهذا السبب غالبًا ما يتجاهلها الفيزيائيون المهتمون بالرياضيات.
بمجرد أن رأينا البيانات من مصادم الهادرونات الكبير، لم أجد أي سبب يُبرر معاملة قوة هيغز بشكل مختلف عن القوى الأخرى. على سبيل المثال، إذا قمت بقياس القوة الكلية بين إلكترونين منفصلين بمسافة قدرها عشر من قطر بروتون، ستجد أنها تتكون من أربع مكونات: أقواها الكهرومغناطيسية وأضعفها الجاذبية، مع قوة هيغز وقوة النواة الضعيفة بينهما. كلٌّ منها على قدم المساواة.

يوضح هذا الرسم التخطيطي على مقياس الحجم الكتل النسبية للكواركات واللبتونات، حيث النيوترينوات هي الجسيمات الأخف و الكوارك العلوي أثقلها. لا يوجد تفسير، ضمن نموذج القياسي وحده، يمكنه حساب هذه القيم الكتلية.